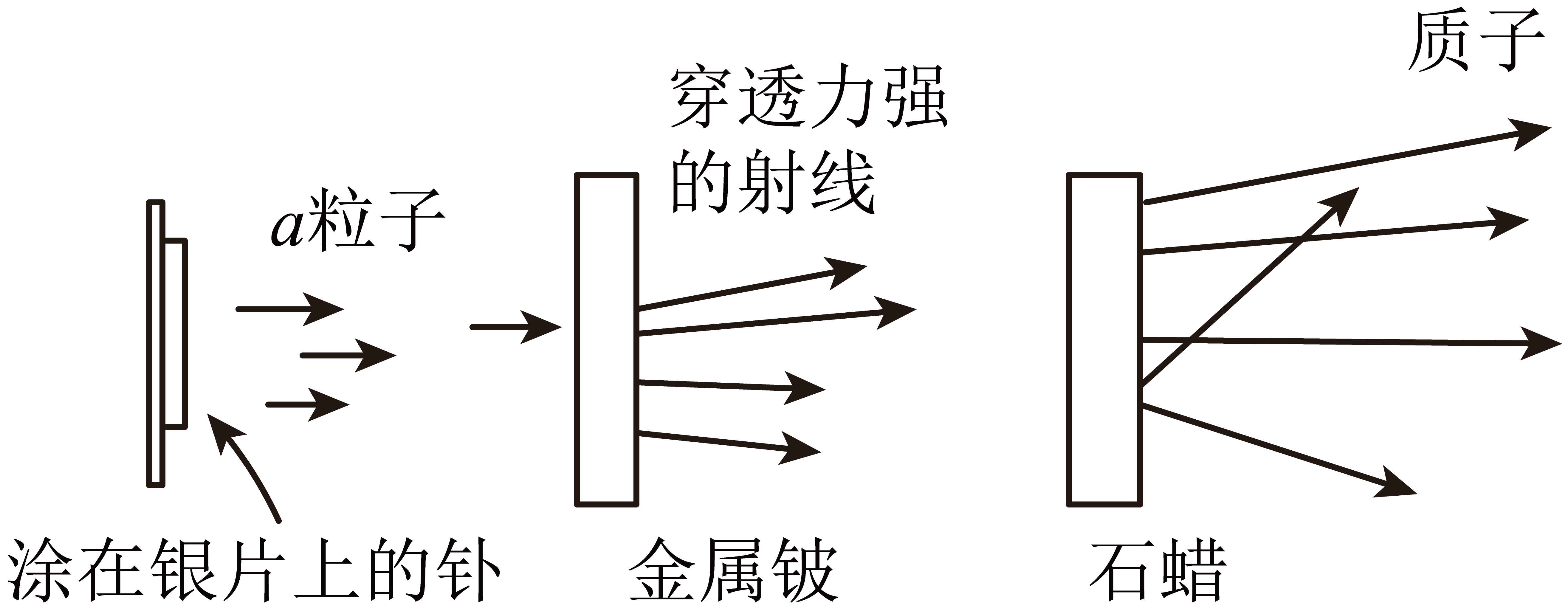
发现中子的核反应方程是$\rm _{4}^{9}Be+{_{2}^{4}He}→$                 。

$\alpha$射线轰击铍，产生不带电的射线是中子，根据质量数与核电荷数守恒可知，其核反应方程为$\rm _{4}^{9}Be+{_{2}^{4}He}→{_{6}^{12}C}+{_{0}^{1}n}$

如图所示，若使石蜡中打出的质子通过障板$ab$上的小孔$o$进入一磁感应强度为$B$的匀强磁场区域。质子在磁场中偏转后落回障板。

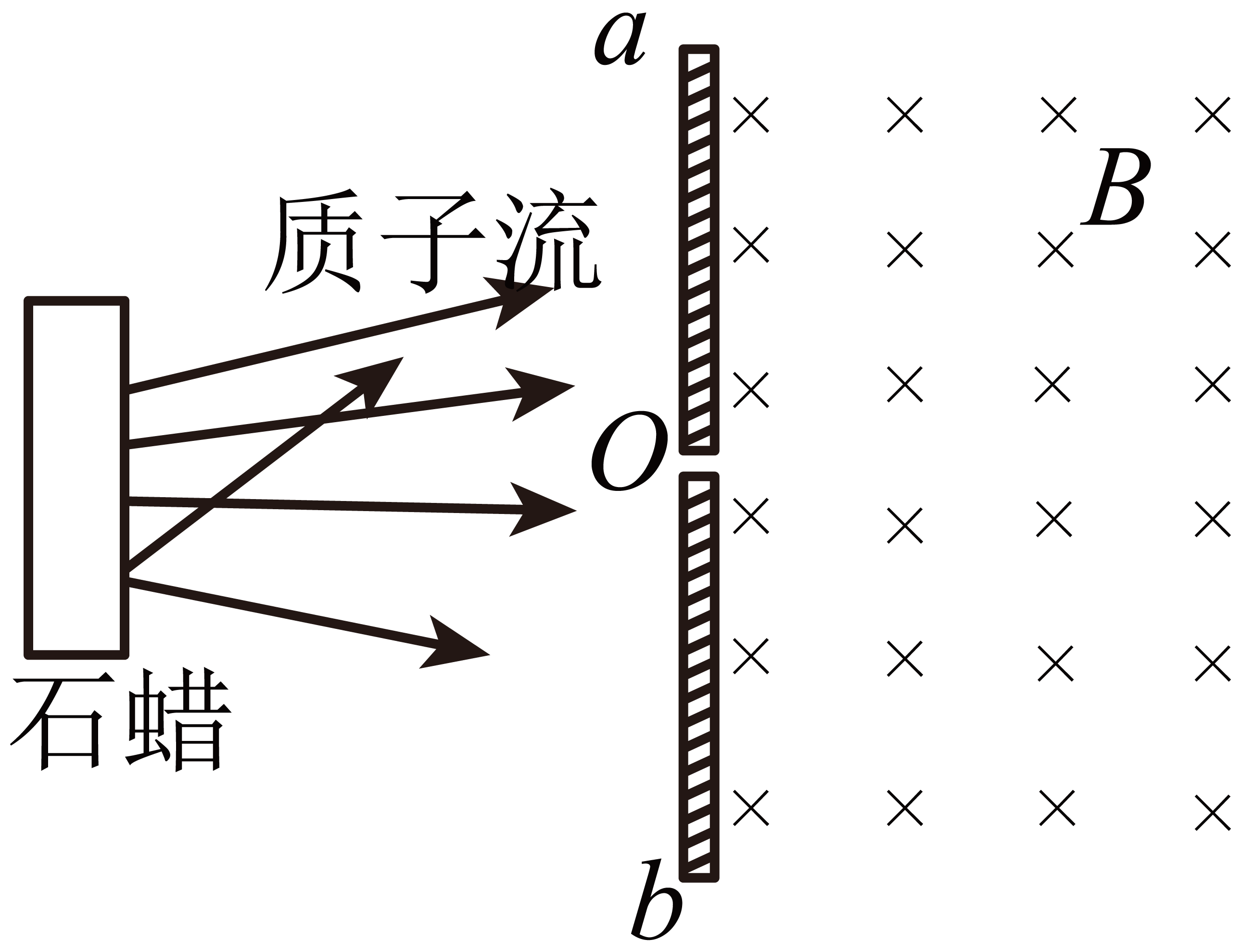
①质子的落点将                   

$\rm A$．仅散布于$oa$间   $\rm B$．仅散布于$ob$间   $\rm C$．在$ab$间均有分布

②已知质子的质量为$m_{p}$，电量为$e$，测得质子落点与小孔$o$之间在沿图中$ab$方向上的最大距离为$D$。则质子进入磁场时的最大速度大小$v=$                 。

③对质量为$m_{p}$、动能为$E$的质子，其德布罗意波长（远小于孔径）可表示为                   

$\rm A$．$h\sqrt{2m_{{p}}E}$ 

$\rm B$．$\dfrac{\sqrt{2m_{{p}}E}}{h}$   

$\rm C$．$\dfrac{h}{\sqrt{2m_{{p}}E}}$

根据左手定则可知，质子在磁场在偏转后散落在$oa$间。

故选：$\rm A$。

由于质子落点与小孔$o$之间在沿图中$ab$方向上的最大距离为$D$，故质子圆周运动的半径$R=\dfrac{1}{2}D$

洛伦兹力提供向心力，则有$Bev=\dfrac{m_{{p}}v^{2}}{R}$

解得$v=\dfrac{eBD}{2m_{{p}}}$

设质子加速后的速度为$v$，则有$\dfrac{1}{2}m_{{p}}v^{2}=E$

根据德布罗意波长公式$\lambda=\dfrac{h}{p}=\dfrac{h}{m_{{p}}v}$

联立解得$\lambda=\dfrac{h}{\sqrt{2m_{{p}}E}}$

故选：$\rm C$。

若使质子沿水平方向进入长度为$L$、场强为$E$的竖直匀强电场区域。标记为①、②的两质子在匀强电场中的偏转轨迹如图所示。忽略电场的边缘效应。

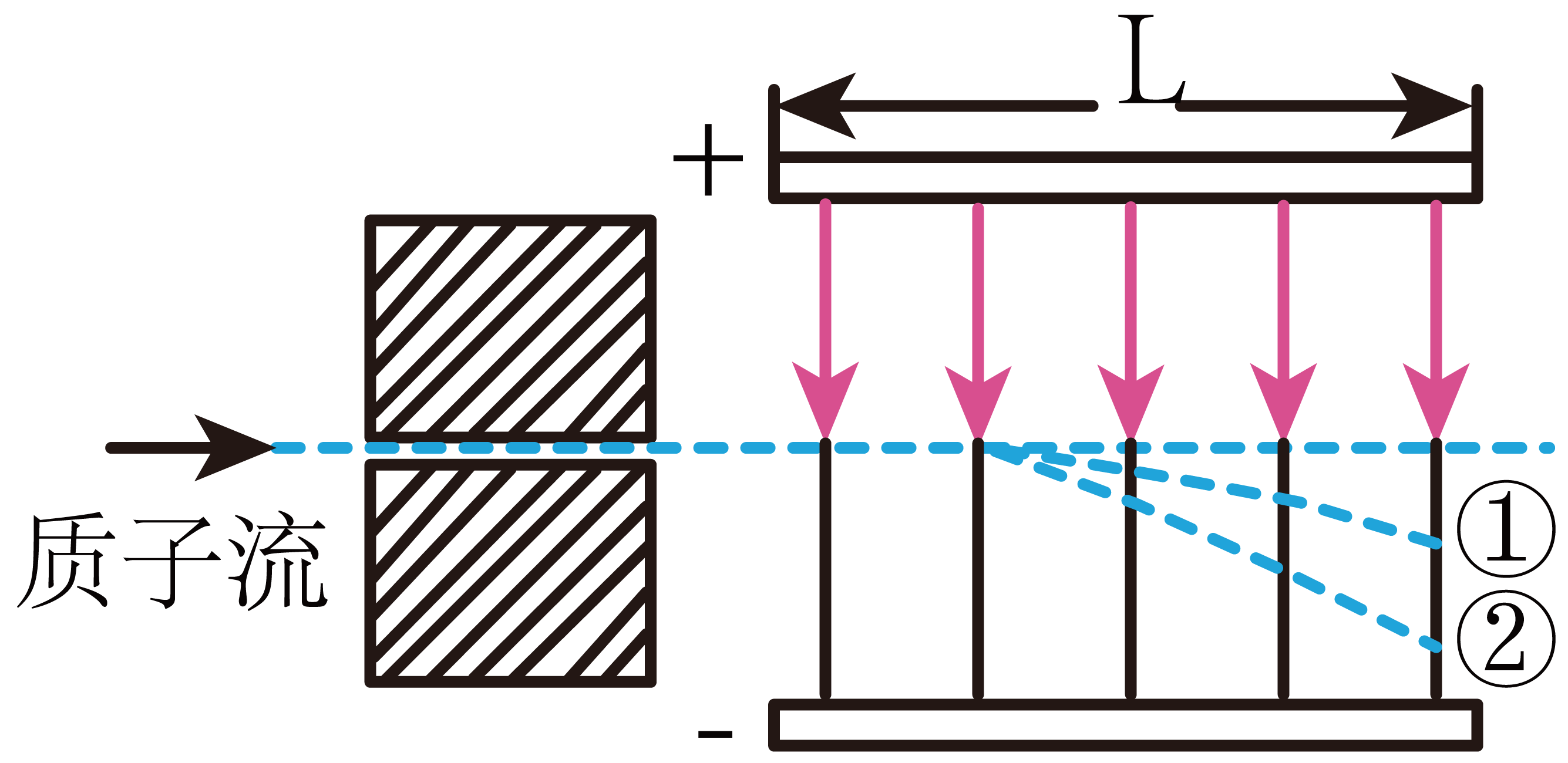
①两质子进入电场时初速度较大的是                 ；穿过电场过程中电势能变化较大的是                 （均选填“①”或“②”）。

②两质子离开电场时的末速度大小能否相等                 。

质子在磁场中做平抛运动，根据平抛运动规律可得$x=v_{0}t$，$y=\dfrac{1}{2}at^{2}$

加速度相同，竖直方向的位移越大运动时间越长，初速度越小，故初速度较大的为①；

电势能的变化量等于电场力所做的功，根据电场力做功$W=qEd$

可知②电场力做功较大，电势能变化量大。

质子做类平抛运动的末速度$v_{t}=\sqrt{v_{0}^{2}+v_{y}^{2}}$

其中$v_{y}=at$，$t=\dfrac{L}{v_{0}}$

可得$v_{t}=\sqrt{{v_{0}}^{2}+\dfrac{a^{2}L^{2}}{{v_{0}}^{2}}}$

若$v_{0}$不同而$v_{t}$等大，应有$v_{1}^{2}+\dfrac{a^{2}L^{2}}{{v_{1}}^{2}}={v_{2}}^{2}+\dfrac{a^{2}L^{2}}{{v_{2}}^{2}}$

解得$v_{1}=v_{2}$（舍）或$v_{1}v_{2}=aL$

故当①、②的初速度大小$v_{1}$、$v_{2}$满足$v_{1}v_{2}=aL=\dfrac{eEL}{m_{p}}$时，①、②末速度等大。

为检验从俄中打出的未知射线是否可能由卢瑟福所预言的中子组成，查德威克假设未知射线中的中性粒子$x$以最大速度$v_{x}$，与石蜡中一初速度可忽略不计氢原子核$p$发生碰撞。碰撞前后系统动量和动能都不变，当碰撞后$p$的速度与$v_{x}$同向时，$p$可获得大小为$v_{p}=3.3\times10^{7}\;\rm m/s$的最大速度。查德威克又用中性粒子$x$轰击氮$(_{7}^{14}\rm N)$核，可使其获得大小为$v_{N}=4.6\times10^{6}\;\rm m/s$的最大速度。求未知中性粒子$x$的质量$m_{x}$与质子质量$m_{p}$之比（保留$2$位有效数字）。

$\\dfrac{m_{x}}{m_{{p}}} \\approx 1.1$

设$x$、$p$的质量分别为$m_{x}$、$m_{p}$。对$x$轰击氢核，碰撞前后系统动量不变$m_{x}v_{x}+0=m_{x}v'_{x}+m_{p}v_{p}$

碰撞前后系统动能不变$\dfrac{1}{2}m_{x}v_{x}^{2}+0=\dfrac{1}{2}m_{x}{v}_{x}'^{2}+\dfrac{1}{2}m_{p}v_{{p}}^{2}$

两式联立，消去$v'_{x}$，可得$\dfrac{v_{{p}}}{v_{x}}=\dfrac{2m_{x}}{m_{x}+m_{{p}}}$

对$x$轰击氢核，同理可得$\dfrac{v_{{N}}}{v_{x}}=\dfrac{2m_{x}}{m_{x}+m_{{N}}}$

则有$\dfrac{v_{{p}}}{v_{{N}}}=\dfrac{m_{{x}}+m_{{N}}}{m_{{x}}+m_{{p}}}=\dfrac{3.3 \times 10^{7}\;\rm \text{m}/\text{s}}{4.6 \times 10^{6}\;\rm \text{m}/\text{s}}$

其中$m_{N}=14m_{p}$

可得$\dfrac{m_{x}}{m_{{p}}} \approx 1.1$