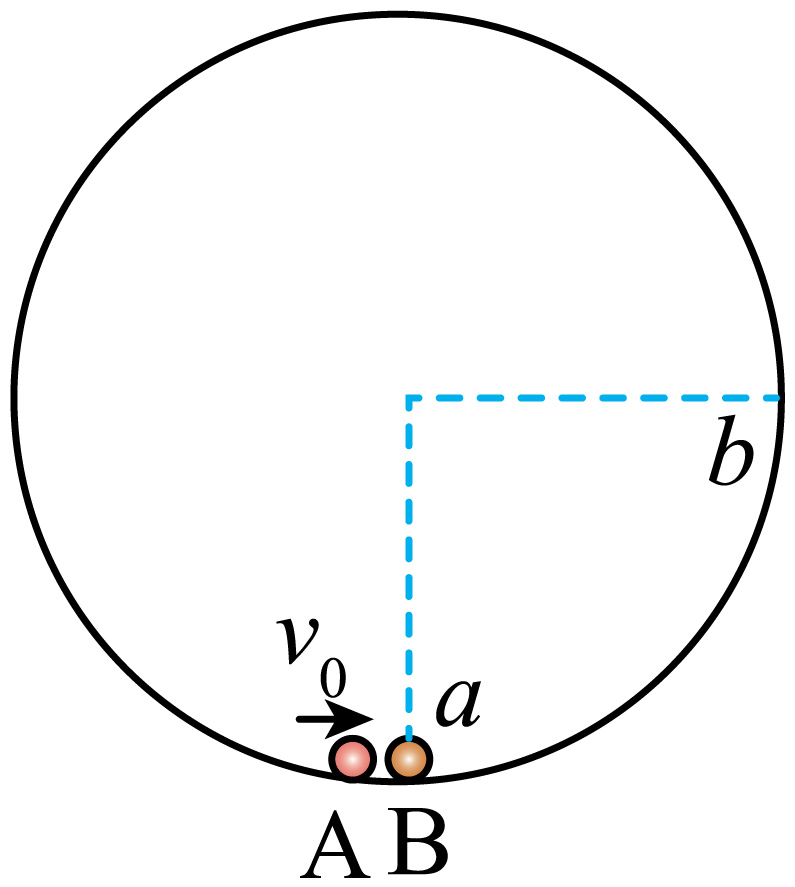
在光滑的水平桌面上固定一个内侧光滑的圆形轨道，俯视图如图所示，$a、b$为圆上两条相互垂直半径的端点。紧贴轨道内侧放置$A、B$两个可视为质点的小球，质量分别为$m、\beta m$，开始时$B$球静止于$a$点，$A$球在其左侧以$v_{0}$的初速度向右与$B$球发生第一次碰撞，随后两球在$b$点发生第二次碰撞。已知小球之间的碰撞均为对心弹性碰撞，则$(\qquad)$

$\\beta$可能为$7$

$\\beta$一定为$7$

若只增大$A$球的质量，则第二次碰撞点可能仍在$b$处

若只增大$A$球的初速度$v_{0}$，则第二次碰撞点一定仍在$b$处

$\rm AB$．设第一次碰后$A$、$B$两球的速度大小分别为$v_{1}$、$v_{2}$，根据动量守恒定律和能量守恒定律有$mv_{0}=mv_{1}+\beta mv_{2}$，$\dfrac{1}{2}mv_{0}^{2}=\dfrac{1}{2}mv_{1}^{2}+\dfrac{1}{2}\beta mv_{2}^{2}$

解得$ v_{1}=\dfrac{m-\beta m}{m+\beta m}v_{0} $，$v_{2}=\dfrac{2m}{m+\beta m}v_{0}$

若碰后$A$、$B$两球反向运动，第二次碰撞发生在$b$点，则有$t=\dfrac{3}{4} \times \dfrac{2\pi R}{- v_{1}}=\dfrac{1}{4} \times \dfrac{2\pi R}{v_{2}}$

联立解得$\beta=7$

若碰后$A$、$B$两球同向运动，第二次碰撞发生在$b$点，则有$t=\dfrac{1}{4} \times \dfrac{2\pi R}{v_{1}}=\dfrac{5}{4} \times \dfrac{2\pi R}{v_{2}}$

联立解得$\beta=0.6$，故$\rm A$正确、$\rm B$错误；

$\rm C$．若碰后$A$、$B$两球反向运动，第二次碰撞发生在$b$点，需满足$\beta=7$，此时增大$A$的质量，使其满足$\beta=0.6$，则第二次碰撞点仍在$b$处，$\rm C$正确；

$\rm D$．相遇的位置由碰后两球速度比决定，由$ v_{1}=\dfrac{m-\beta m}{m+\beta m}v_{0}$，$v_{2}=\dfrac{2m}{m+\beta m}v_{0}$

得$\dfrac{v_{1}}{v_{2}}=\dfrac{m-\beta m}{2m}$

可知速度比与$v_{0}$无关，若只增大$A$球的初速度$v_{0}$，则第二次碰撞点一定仍在$b$处，故$\rm D$正确。

故选：$\rm ACD$。