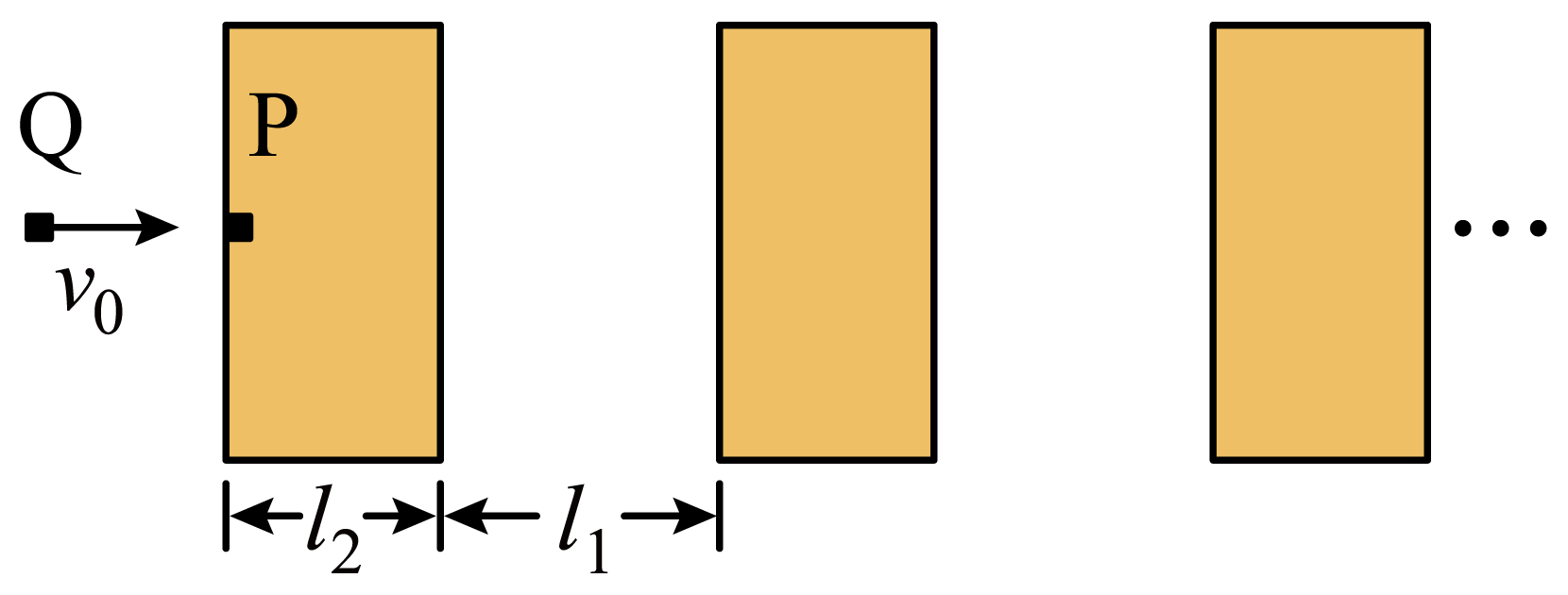
该碰撞过程中损失的机械能；

$24.5\\;\\rm J$

$P$、$Q$与发生正碰，由动量守恒定律$m_{2}v_{0}=m_{2}v_{\rm Q}+m_{1}v$

由能量守恒定律$\dfrac{1}{2}m_{2}v_{0}^{2}=\dfrac{1}{2}m_{2}v_{\text{Q}}^{2}+\dfrac{1}{2}m_{1}v^{2}+\Delta E$

联立可得$v_{\rm Q}=3.5\;\rm m/s$，$\Delta E=24.5\;\rm J$

$P$从开始运动到静止经历的时间。

$5\\;\\rm s$

对物块$P$受力分析由牛顿第二定律$\mu m_{1}g=m_{1}a$

物块$P$在第一个防滑带上运动时，由运动学公式$v^{2}-v_{\rm P1}^{2}=2al_{2}$，$v_{\rm P1}=v-at_{1}$

解得$v_{\rm P1}=5\;\rm m/s$

则物块$P$在第一个防滑带上运动的时间为$t_{1}=0.4\;\rm s$

物块$P$在光滑的直道上做匀速直线运动，则$l_{1}=v_{\rm P1}t_{2}$

解得$t_{2}=0.6\;\rm s$

物块$P$在第二个防滑带上运动时，由运动学公式$v_{\rm P1}^{2}-v_{\rm P2}^{2}=2al_{2}$，$v_{\rm P2}=v_{\rm P1}-at_{3}$

解得$v_{\rm P2}=1\;\rm m/s$

则物块$P$在第二个防滑带上运动的时间为$t_{3}=0.8\;\rm s$

物块$P$在光滑的直道上做匀速直线运动，则$l_{1}=v_{P2}t_{4}$

解得$t_{4}=3\;\rm s$

由以上条件可知，物块$P$最终停在第三个防滑带上，由运动学公式$0=v_{\rm P2}-at_{5}$

可得物块$P$在第三个防滑带上运动的时间为$t_{5}=0.2\;\rm s$

故物块$P$从开始运动到静止经历的时间为$t=t_{1}+t_{2}+t_{3}+t_{4}+t_{5}=5\;\rm s$