高中 | 匀变速直线运动的速度位移公式 题目答案及解析
稿件来源:高途
高中 | 匀变速直线运动的速度位移公式题目答案及解析如下,仅供参考!
必修1
第二章 匀变速直线运动的研究
2.4 匀变速直线运动的速度与位移的关系
匀变速直线运动的速度位移公式
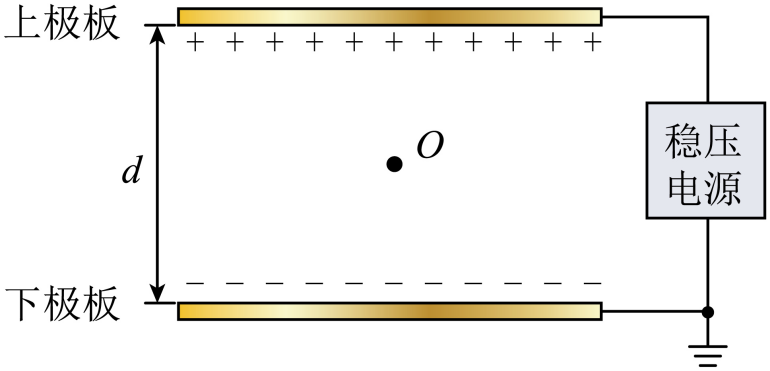
如图所示,真空中固定放置两块较大的平行金属板,板间距为$d$,下极板接地,板间匀强电场大小恒为$E$。现有一质量为$m$、电荷量为$q$($q \gt 0$)的金属微粒,从两极板中央$O$点由静止释放。若微粒与极板碰撞前后瞬间机械能不变,碰撞后电性与极板相同,所带电荷量的绝对值不变。不计微粒重力。求:
微粒第一次到达下极板所需时间;
$\\sqrt{\\dfrac{md}{qE}}$;
"]]由牛顿第二定律$qE=ma$
由运动学公式$\dfrac{d}{2}=\dfrac{1}{2}at^{2}$
联立可得微粒第一次到达下极板所需的时间为$t=\sqrt{\dfrac{md}{qE}}$;
微粒第一次从上极板回到$O$点时的动量大小。
$2\\sqrt{qEmd}$。
"]]微粒第一次到达下极板时的速度大小为$v_{1}=at=\sqrt{\dfrac{qEd}{m}}$
由于微粒与极板碰撞前后瞬间机械能不变,碰撞后电性与极板相同,所带电荷量的绝对值不变,设微粒碰后第一次到达上极板时的速度大小为$v_{2}$,满足$v_{2}^{2} − v_{1}^{2}=2ad$
代入解得$v_{2}=\sqrt{\dfrac{3qEd}{m}}$
同理可得微粒第一次从上极板回到$O$点时的速度大小为$v_{3}$,满足$v_{3}^{2}-v_{2}^{2}=2a\dfrac{d}{2}$
代入解得$v_{3}=2\sqrt{\dfrac{qEd}{m}}$
故微粒第一次从上极板回到$O$点时的动量大小为$p=mv_{3}=2\sqrt{qEmd}$。
高中 | 匀变速直线运动的速度位移公式题目答案及解析(完整版)
