高中 | 闭合电路的欧姆定律基本问题 题目答案及解析
稿件来源:高途
高中 | 闭合电路的欧姆定律基本问题题目答案及解析如下,仅供参考!
选修3-1
第二章 恒定电流
2.7 闭合电路的欧姆定律
闭合电路的欧姆定律基本问题
磁场作为一种物质的存在形态,广泛存在于宇宙甚至生物体内,人类生活中处处可以遇到磁场,随着科学的发展,磁技术已经渗透到了我们日常生活和工农业生产技术的各个方面。请完成下列问题:
如图为用电流天平原理测磁场的示意图,等臂天平左端挂有长方形线圈$abcd$共 $10$匝。线圈底边$bc$水平,长为$8\;\rm cm$,磁场方向垂直线圈平面向外。首先让线框内通入$0.5\;\rm A$的电流,并在天平右侧加上砝码,使天平平衡。保持电流大小不变,改变电流方向,右盘中减少了$40g$砝码后,天平再次平衡。则第一次平衡时$bc$边上的电流方向是 (“向左”或者“向右”),磁感应强度大小$B=$ $T$;($g=9.8\;\rm m/s^{2}$)
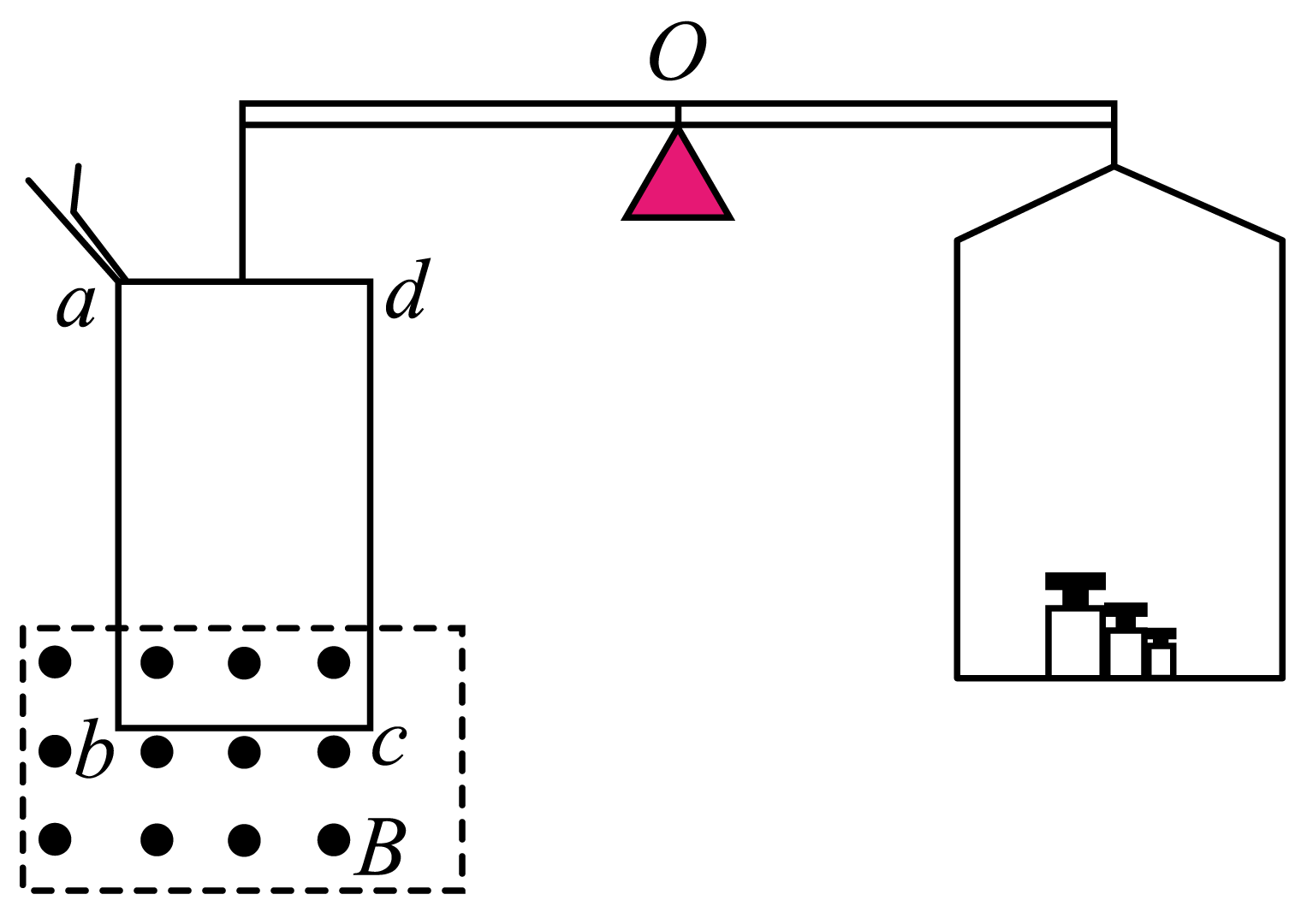
改变电流方向后,减少右盘中砝码天平才能够平衡,表明改变电流后底边所受安培力方向向上,则改变电流方向之前底 所受安培力方向向下,根据左手定则可知,第一次平衡时$bc$边上的电流方向是向右;
结合上述,改变电流方向之前,根据平衡条件有$nBIL+m_{左}g=m_{右}g$
改变电流方向之后,根据平衡条件有$m_{左}g − nBIL=(m_{右} − \Delta m)g$
解得$B=0.49T$;
利用霍尔原理可以制作磁传感器。如图为某霍尔元件测量原理示意图。将一块边长为$L$厚度为$d$的正方形半导体薄片放在匀强磁场中,磁场方向垂直于薄片向下,$a$、$b$和$M$、$N$为相互两两正对的四个电极。在$a$、$b$间通入图示恒定电流,则薄片内电量为$e$ 的自由电子在洛伦兹力的作用下,将在两侧形成电荷堆积。稳定后在$M$、$N$两极形成电势差$U$。
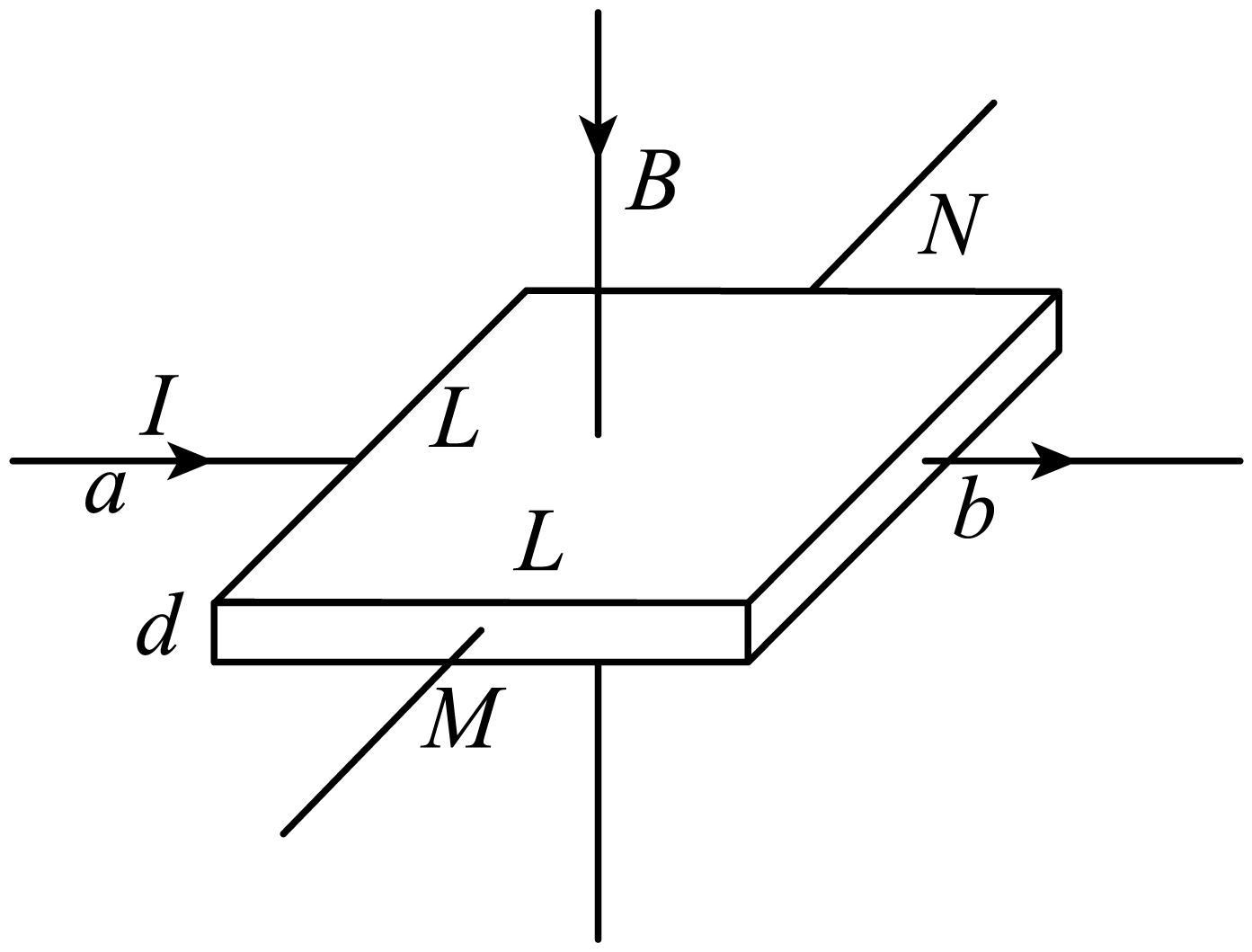
Ⅰ$.$在$M$、$N$两极电势较高的是 极;
Ⅱ$.$计算:若$a$、$b$间通入的电流强度为$I$,半导体单位体积内的自由电子数为$n$。求
①自由电子移动的平均速率$v=$ ;
②磁感强度$B$ 的大小 ;
电流方向向右,电子带负电,则电子定向移动方向向左,根据左手定则可知,电子在洛伦兹力作用下向$\rm N$极聚集,可知,电势较高的是$M$极;
$a$、$b$间通入的电流强度为$I$,根据电流的微观定义式有$I=nevS$
其中$S=Ld$
解得$v=\dfrac{I}{nedL}$
稳定时,电子所受洛伦兹力与电场力平衡,则有$evB=e\dfrac{U}{L}$
结合上述解得$B=\dfrac{nedU}{I}$;
如图所示是一个简易交流发电机原理图。手摇转盘,通过皮带传动带动转轴转动(皮带不打滑),矩形线圈$abcd$垂直于纸面处于水平方向匀强磁场中,且与转轴同轴转动。线圈在匀速转动时输出周期$T=0.2\;\rm s$,电动势最大值$E_{\rm{m}}= 2\sqrt{2}\;\rm{V}$的正弦交流电。已知转盘和转轴的半径之比$n=10:1$,线圈内阻$r=2\;\rm \Omega$。
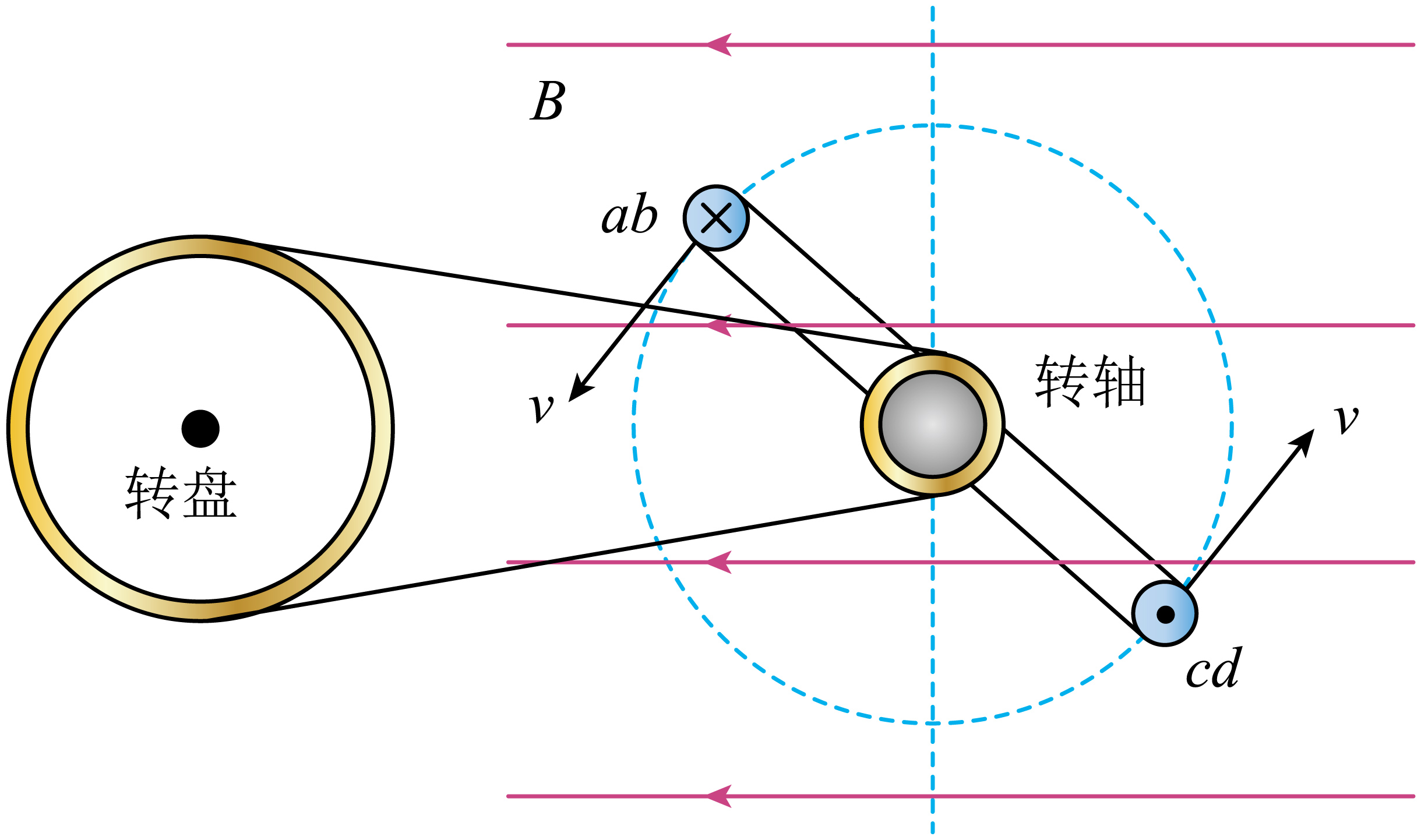
Ⅰ$.$手摇转盘的角速度$\omega=$ $\;\rm rad/s$。当线圈平面转到图示的中性面位置时,线圈内的磁通量最 ,磁通量变化率最 (填“大”或“小”);
Ⅱ$.$从线圈处于图示位置开始计时,且该时刻的电流方向规定为正方向。
①判断磁场的方向 (“向左”或“向右”)。
②该电动势$e$ 随时间变化的图像可能正确的是
$\rm A$.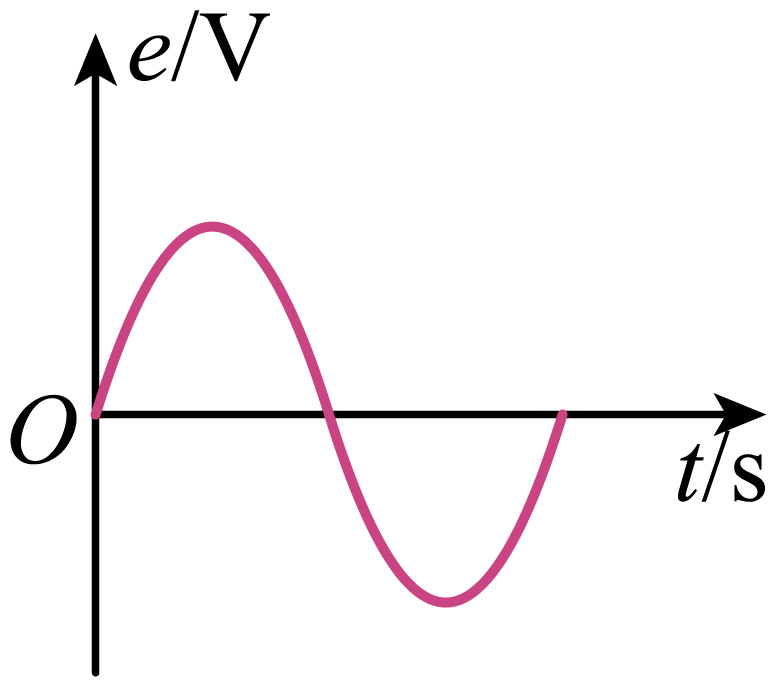 $\rm B$.
$\rm B$.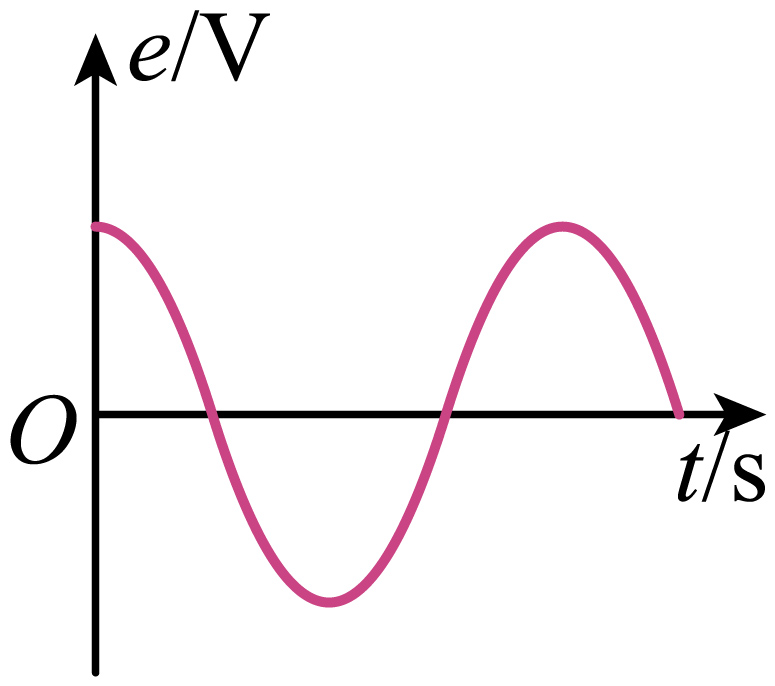
$\rm C$.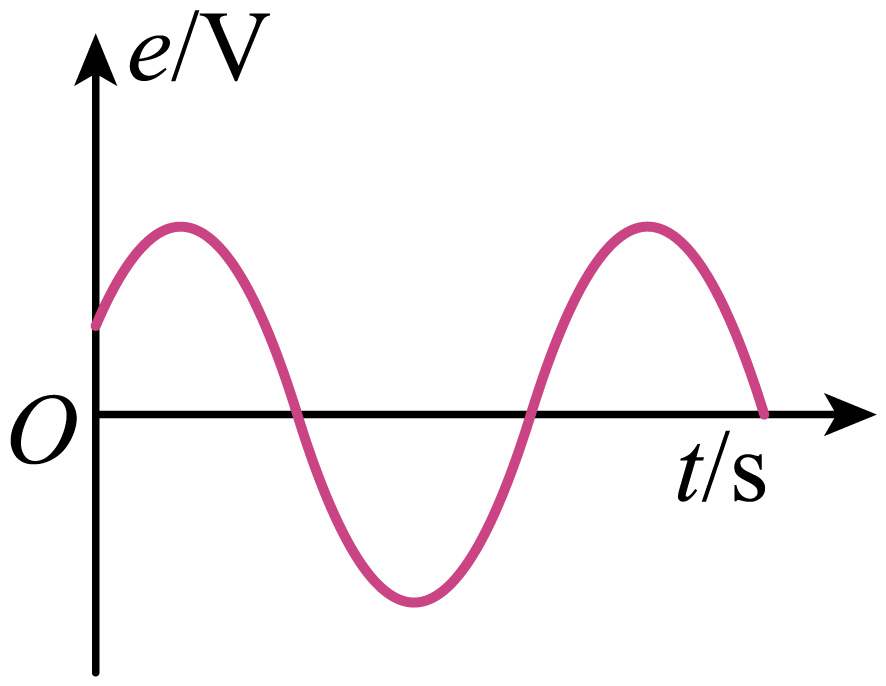 $\rm D$.
$\rm D$.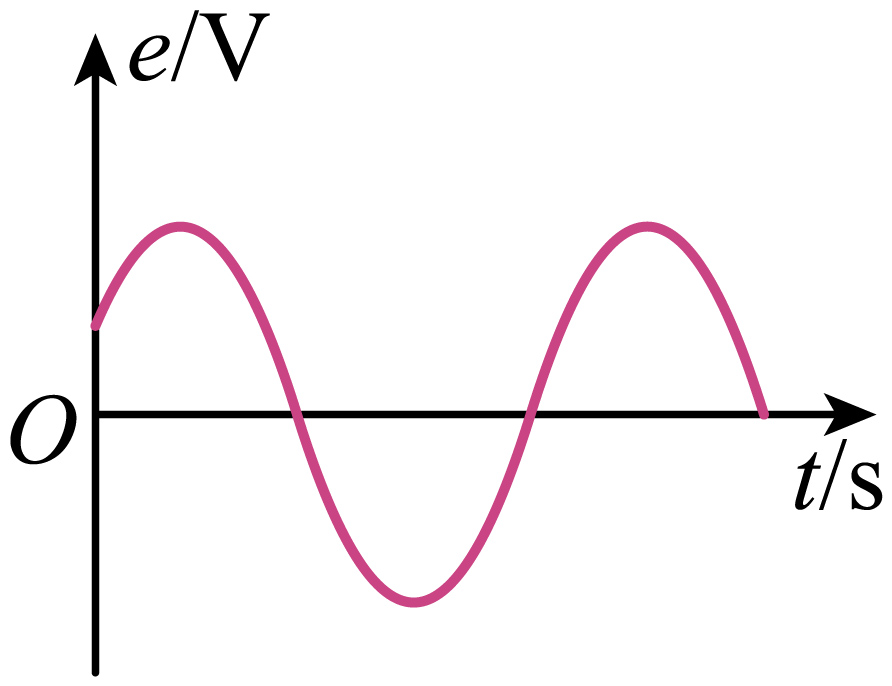
③计算:在输出端接入一个$R=18\;\rm \Omega$的电阻,手摇转盘$10$圈时间内,发电机的输出功为多少 ?
转轴转动的角速度$\omega_{0}=\dfrac{2\pi}{T}$
转轴边缘与转盘边缘线速度大小相等,则有$\omega R_{盘}=\omega_{0}R_{轴}$
其中$\dfrac{R_{盘}}{R_{轴}}=\dfrac{10}{1}$
解得$\omega=\pi \:\rm rad/s$
当线圈平面转到图示的中性面位置时,线圈内的磁通量最大,磁通量变化率最小。
根据右手定则可知,磁场的方向水平向左。
$\rm AB$.图示计时起点的位置不是中性面,结合上述可知,计时起点的电动势不等于$0$,故$\rm AB$错误;
$\rm CD$.图示位置电动势为正值,由计时起点到 到达中性面经历时间大于四分之一个周期,到达中性面后电动势方向发生改变,故$\rm C$错误,$\rm D$正确。
故选:$\rm D$。
转盘转动$10$圈所用时间$t=\dfrac{\theta}{\omega}=\dfrac{20\pi}{\pi}=20\;\rm {s}$
电动势的有效值$E=\dfrac{E_{\rm {m}}}{\sqrt{2}}=2\;\rm{V}$
根据闭合电路欧姆定律有$I=\dfrac{E}{R+r}=0.1\;\rm{A}$
则输出功为$W=IUt=I^{2}Rt=3.6\;\rm J$。
高中 | 闭合电路的欧姆定律基本问题题目答案及解析(完整版)
