如图为平行板电容器充电过程中板间电压$U$与电荷量$Q$的图像。

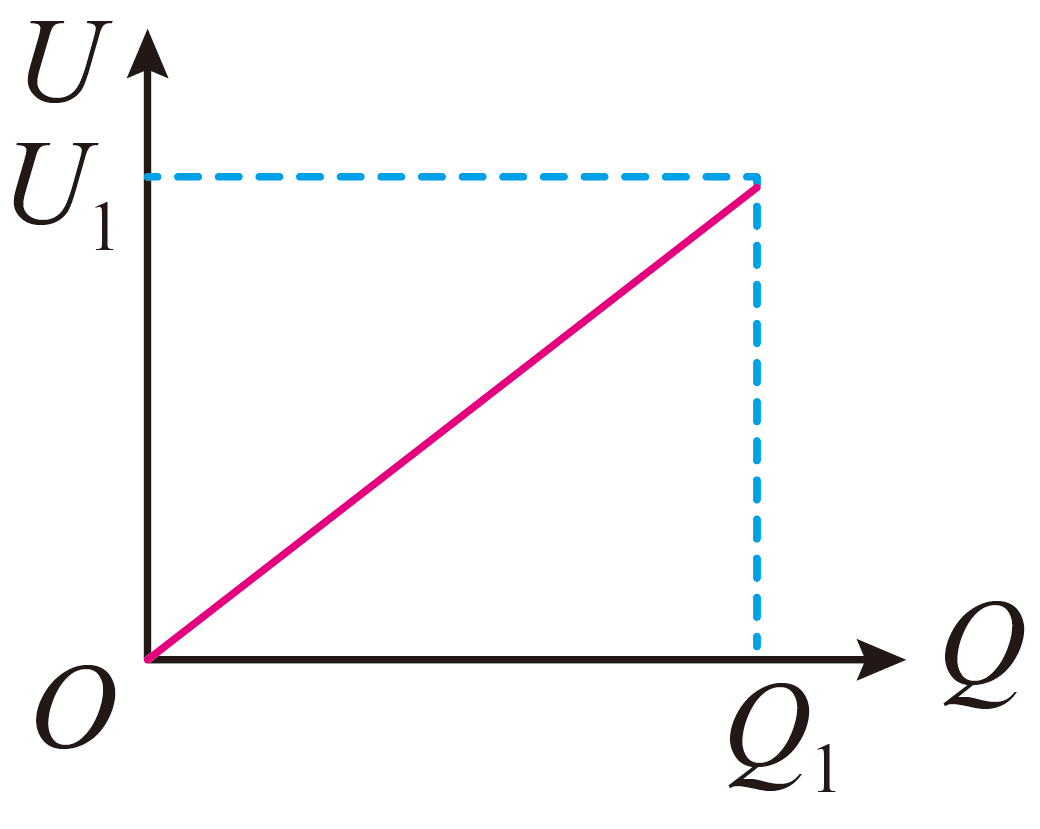
①根据$U-Q$图像，若电容器充满电时电荷量为$Q_{1}$，板间电压为$U_{1}$。则电容器储存的电势能为                 。

②减小电容器的极板间距，图线斜率将                 。

$\rm A$．增大                 $\rm B$．不变                 $\rm C$．减小

①由$U-Q$图像与横轴围成的面积表示电容器储存的电势能，则$E=\dfrac{1}{2}Q_{1}U_{1}$

②根据$U=\dfrac{1}{C}Q$可知$U − Q$图像的斜率为$k=\dfrac{1}{C}$，根据电容的决定式$C=\dfrac{\varepsilon S}{4\pi kd}$可得减小电容器的极板间距，故电容$C$增大，故图线的斜率减小。

故选：$\rm C$。

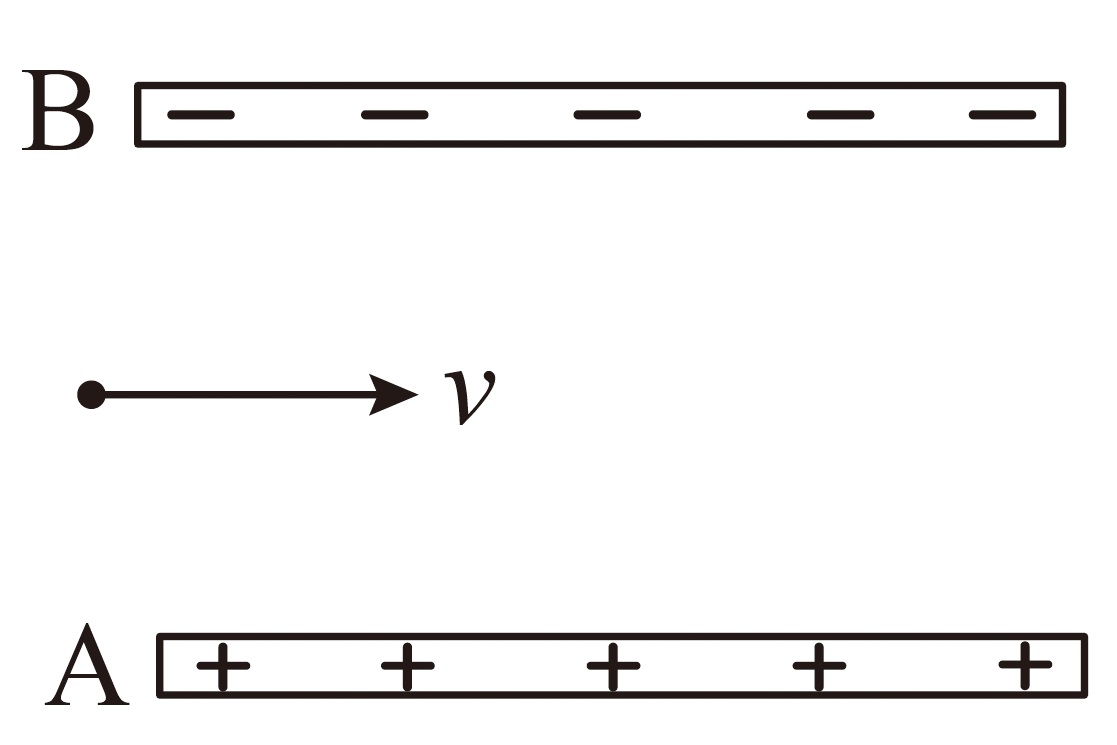
（计算）如图，$A$、$B$为平行板电容器的两极板，板长为$L$，板间距为$d$，电容器电容为$C$，带电量为$Q$。一电子从两极板左侧正中央水平向右射入。已知电子电荷量为$e$，质量为$m$。求电子能从两极板间飞出的最小初速度$v$。

$\\dfrac{L}{d}\\sqrt{\\dfrac{Qe}{Cm}}$

粒子在电场中做类平抛运动，其板间电压为$U=\dfrac{Q}{C}$，电场强度$E=\dfrac{U}{d}$，对电子由牛顿第二定律$eE=ma$

可得电子的加速度为$a=\dfrac{eQ}{Cmd}$

电子在水平方向做匀速直线运动，则$L=vt$

若此时电子恰好能从极板边缘射出，对应的初速度最小，由电子在竖直方向做初速度为零的匀加速直线运动，有$y=\dfrac{d}{2}=\dfrac{1}{2}at^{2}$

联立可得，电子能从两极板间飞出的最小初速度为$v=\dfrac{L}{d}\sqrt{\dfrac{Qe}{Cm}}$

某同学制作一个电池，并连接如图所示的电路。电池的电动势为$E=10\;\rm V$，内阻为$r=200\;\rm \Omega$，定值电阻$R_{1}=100\;\rm \Omega$。滑动变阻器$R$的阻值范围为$0\sim 100\;\rm \Omega$。

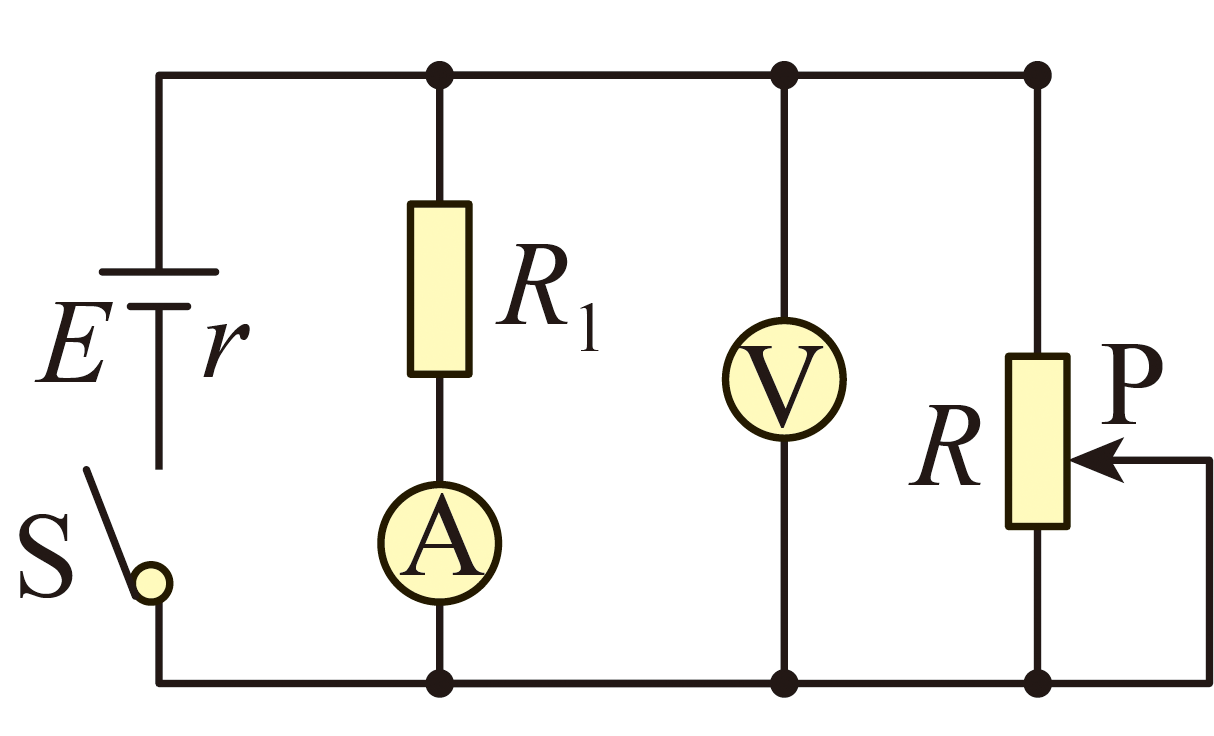
①闭合开关$\rm S$后，滑动变阻器$R$的滑片向上移动过程中，电流表示数                 。

$\rm A$．减小       $\rm B$．增大       $\rm C$．先增大后变小       $\rm D$．先变小后增大

②电池输出功率最大时，滑动变阻器阻值为                 $\;\rm \Omega$，电压表示数为                 $\;\rm V$。

①闭合开关$\rm S$后，滑动变阻器$R$的滑片向上移动过程中，滑动变阻器$R$的阻值减小，总电阻减小，由闭合电路欧姆定律可知电路中总电流增大，电源内电压$U_{内}=Ir$增大，则路端电压$U=E-Ir$减小，电流表示数$I_{1}=\dfrac{U}{R_{1}}$减小。

故选：$\rm A$。

②电源的输出功率$P_{出}={\left(\dfrac{E}{R_{外}+r}\right)}^{2}R_{外}=\dfrac{E^{2}}{\dfrac{{(R_{外}-r)}^{2}}{R_{外}}+4r}$

当$R_{外}=r$时电源的输出功率最大，但$R_{外\max}=\dfrac{RR_{1}}{R+R_{1}}=50\;\rm \Omega\lt r=200\;\rm \Omega$

所以当滑动变阻器阻值为$R=100\;\rm \Omega$时，电源的输出功率最大。

电压表的示数为$U=\dfrac{E}{R_{外\max}+r}R_{外\max}=\dfrac{10}{50+200} \times 50\;\rm \text{V}=2\;\rm \text{V}$