| 闭合电路的欧姆定律基本问题 题目答案及解析
稿件来源:高途
| 闭合电路的欧姆定律基本问题题目答案及解析如下,仅供参考!
选修3-1
第二章 恒定电流
2.7 闭合电路的欧姆定律
闭合电路的欧姆定律基本问题
如图所示为一个小型旋转电枢式交流发电机的原理图,其矩形线圈的$ab$边长为$0.25\;\rm m$,$bc$边长为$0.20\;\rm m$,共有$n=100$匝,总电阻$r=1.0\;\rm \Omega$,可绕与磁场方向垂直的对称轴$OO^\prime$转动。线圈处于磁感应强度$B=0.40\;\rm T$的匀强磁场中,与线圈两端相连的金属滑环上接一个“$3.0\;\rm V$,$1.8\;\rm W$”的灯泡,当线圈以角速度$\omega$匀速转动时,小灯泡消耗的功率恰好为$1.8\;\rm W$。(不计转动轴与电刷的摩擦,结果保留两位有效数字)
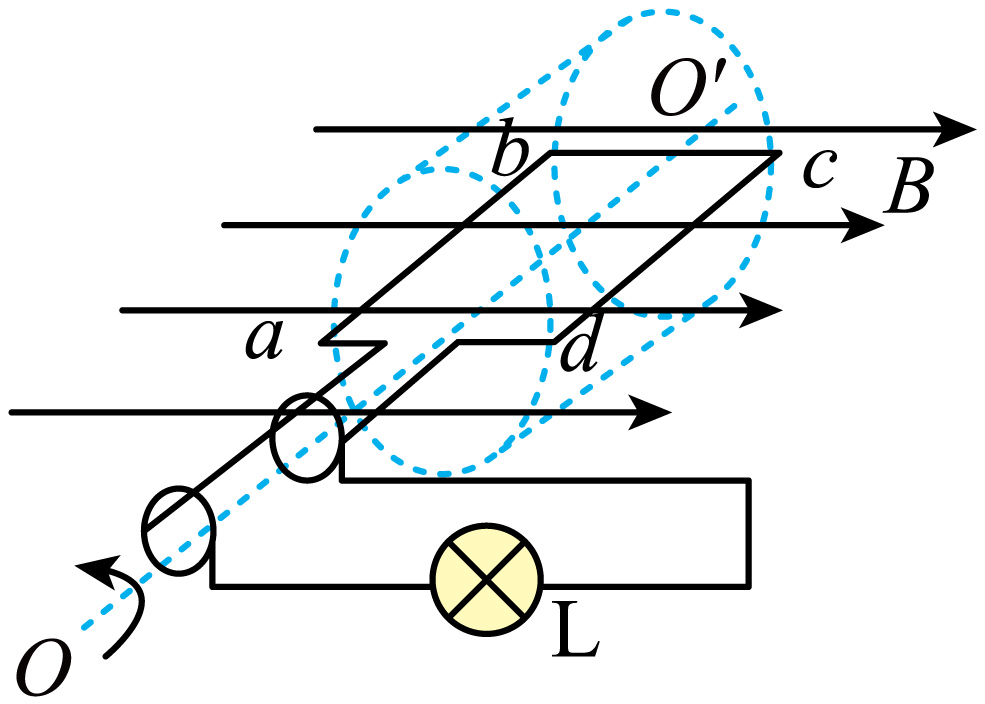
求发电机感应电动势的有效值;
$3.6\\;\\rm V$
"]]设小灯泡正常发光时的电流为$I$,则$I=\dfrac{P_{额}}{U_{额}}=0.60\;\rm \text{A}$
设灯泡正常发光时的电阻为$R$,$R=\dfrac{U_{额}^{2}}{P}=5.0\;\rm \Omega$
再根据闭合电路的欧姆定律有$E=I(R+r)=3.6\;\rm V$
求线圈转动的角速度$\omega$;
$2.5\\;\\rm rad/s$
"]]发电机感应电动势最大值为$E_{{m}}=\sqrt{2}E$,$E_{m}=nBS\omega$
解得$\omega=\dfrac{E_{{m}}}{nBS}=2.5\;\text{rad/s}$
线圈以上述角速度转动$100$周过程中发电机产生的电能为多少。
$5.4\\times10^{2}\\;\\rm J$
"]]发电机产生的电能为$Q=EIt$,$t=100\dfrac{2\pi}{\omega}$
解得$Q=5.4\times10^{2}\;\rm J$
| 闭合电路的欧姆定律基本问题题目答案及解析(完整版)
