| 闭合电路的欧姆定律基本问题 题目答案及解析
稿件来源:高途
| 闭合电路的欧姆定律基本问题题目答案及解析如下,仅供参考!
选修3-1
第二章 恒定电流
2.7 闭合电路的欧姆定律
闭合电路的欧姆定律基本问题
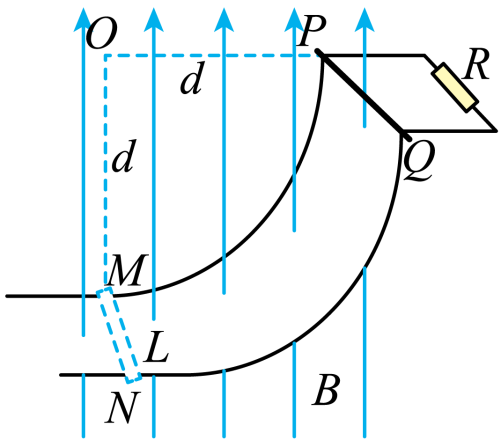
如图所示,$PM$、$QN$是两根半径为$d$的粗糙的$\dfrac{1}{4}$圆弧轨道,其间距为$l$,$O$点为$PM$圆弧的圆心,$O$、$P$连线水平,$M$、$N$在同一水平高度,圆弧轨道电阻不计,在其上端连有一阻值为$R$的电阻,整个装置处于竖直向上的匀强磁场中,磁感应强度大小为$B$。现有一根长度稍大于$l$、质量为$m$、电阻为$r$的金属棒从轨道的顶端$PQ$处以一定的初速度开始下滑,由于轨道摩擦的作用,下滑过程中金属棒的速率保持不变,到达轨道底端$MN$时对轨道的压力为$2mg$,求:
金属棒到达最低点时它两端的电压;
$\\dfrac{RBl\\sqrt{gd}}{R+ r}$;
"]]在轨道的最低点$MN$处,金属棒对轨道的压力$F_{N}=2mg$
根据牛顿第三定律知轨道对金属棒的支持力大小$F'_{N}=F_{N}=2mg$
根据牛顿第二定律${F'}_{{N}}-mg=\dfrac{mv^{2}}{d}$
解得$v=\sqrt{gd}$
金属棒切割磁感线产生的感应电动势$E=Blv$
金属棒到达最低点时两端的电压$U=\dfrac{R}{R+r}E=\dfrac{RBl\sqrt{gd}}{R+r}$;
金属棒由$PQ$下滑到$MN$过程中通过它的电荷量;
$\\dfrac{Bld}{R+r}$;
"]]由金属棒由$PQ$下滑到$MN$过程中通过它的电荷量$q=\overline{I}\Delta t$
又
$\overline{I}=\dfrac{\overline{E}}{R+r}$,$\overline{E}=\dfrac{\Delta\Phi}{\Delta t}$,$\Delta\Phi=Bld$
联立解得$q=\dfrac{Bld}{R+r}$;
由$PQ$下滑到$MN$过程中金属棒中产生的焦耳热。
$\\dfrac{\\pi B^{2}l^{2}dr\\sqrt{gd}}{4{(R+ r)}^{2}}$。
"]]下滑过程中,金属棒切割磁感应线产生正弦式交流电,其有效值$E_{有效}=\dfrac{E_{\rm{m}}}{\sqrt{2}}=\dfrac{Bl\sqrt{gd}}{\sqrt{2}}$
回路中产生的焦耳热$Q=\dfrac{\left( E_{有效} \right)^{2}}{(R+r)} \cdot \dfrac{\pi d}{2v}=\dfrac{\pi B^{2}l^{2}d\sqrt{gd}}{4(R+r)}$
金属棒产生的热量$Q_{1}=\dfrac{r}{R+r}Q=\dfrac{\pi B^{2}l^{2}dr\sqrt{gd}}{4{(R+r)}^{2}}$。
| 闭合电路的欧姆定律基本问题题目答案及解析(完整版)
