| 闭合电路的欧姆定律基本问题 题目答案及解析
稿件来源:高途
| 闭合电路的欧姆定律基本问题题目答案及解析如下,仅供参考!
选修3-1
第二章 恒定电流
2.7 闭合电路的欧姆定律
闭合电路的欧姆定律基本问题
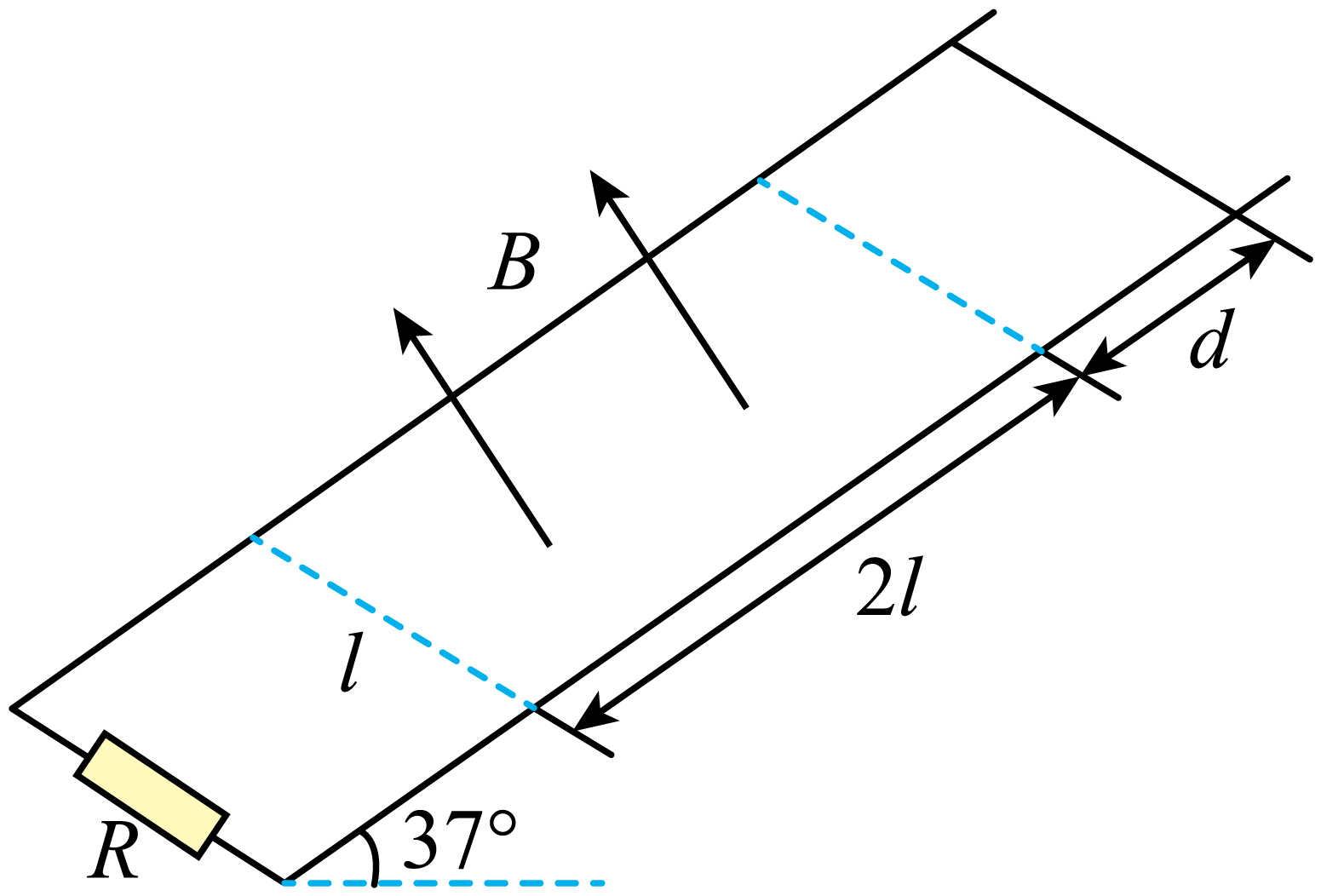
如图所示,两平行金属导轨间距为$l=0.5m$下端连接阻值为$R=2\;\rm \Omega$的定值电阻,两导轨形成的斜面倾角$\theta=37^\circ $,两导轨之间有一长度为$2l$的匀强磁场区域,磁感应强度的大小为$B=kt$($k$为大于$0$的常数),方向垂直于斜面向上,图中两条虚线为磁场的边界。现将质量$m=1\;\rm kg$、电阻$r=2\;\rm \Omega$、长度为$l$的金属棒由静止放置在导轨上,金属棒与导轨间的动摩擦因数$\mu =0.5$,金属棒初位置与磁场边界的距离为$d=1m$。在$t=0$时刻释放金属棒,它沿导轨匀加速下滑,当它进入磁场的瞬间,磁场开始保持不变,金属棒恰好能匀速下滑,已知重力加速度$g$取$10\;\rm m/s^{2}$,$\sin37^\circ =0.6$。求:
$k$的数值;
$4$;
"]]导体棒由静止开始下滑,根据牛顿第二定律有$mg\sin\theta − \mu mg\cos\theta=ma$
设刚进入磁场时速度大小为$v$,根据速度位移公式有$v^{2}=2ad$
解得$a=2\;\rm m/s^{2}$,$v=2\;\rm m/s$
刚进入磁场时,设电动势大小为$E$,根据法拉第电磁感应定律有$E=Blv$
根据闭合电路欧姆定律有$I=\dfrac{E}{r+R}$
导体棒受力平衡$mg\sin\theta − \mu mg\cos\theta=BIl$
解得$B=4T$
金属棒从释放到进入磁场的时间$t=\dfrac{v}{a}=1\;\rm{s}$
由$B=kt$
解得$k=4$;
金属棒进入磁场前后的电流大小的比值;
$\\dfrac{1}{2}$;
"]]根据法拉第电磁感应定律,金属棒进入磁场前的感应电动势$E_{0}=\dfrac{\Delta\Phi}{\Delta t}=S \cdot \dfrac{\Delta B}{\Delta t}=8l^{2}=2\;\rm{V}$
感应电流$I_{0}=\dfrac{E_{0}}{R+r}=0.5\;\rm{A}$
进入磁场后感应电流大小为$I=\dfrac{E}{R+r}=1\;\rm{A}$
所以$\dfrac{I_{0}}{I}=\dfrac{1}{2}$;
金属棒下滑过程中定值电阻$R$产生的焦耳热。
$1.5\\;\\rm J$。
"]]导体棒进入磁场前,定值电阻中产生的热量$Q_{0}=I_{0}^{2}Rt$
解得$Q_{0}=0.5\;\rm J$
导体棒进入磁场后,定值电阻中产生的热量$Q=I^{2}Rt'$
其中$t'=\dfrac{2l}{v}=0.5\;\rm{s}$
解得$Q=1\;\rm J$
所以金属棒下滑过程中定值电阻$R$产生的焦耳热$Q_{1}=Q_{0}+Q=1.5\;\rm J$。
| 闭合电路的欧姆定律基本问题题目答案及解析(完整版)
