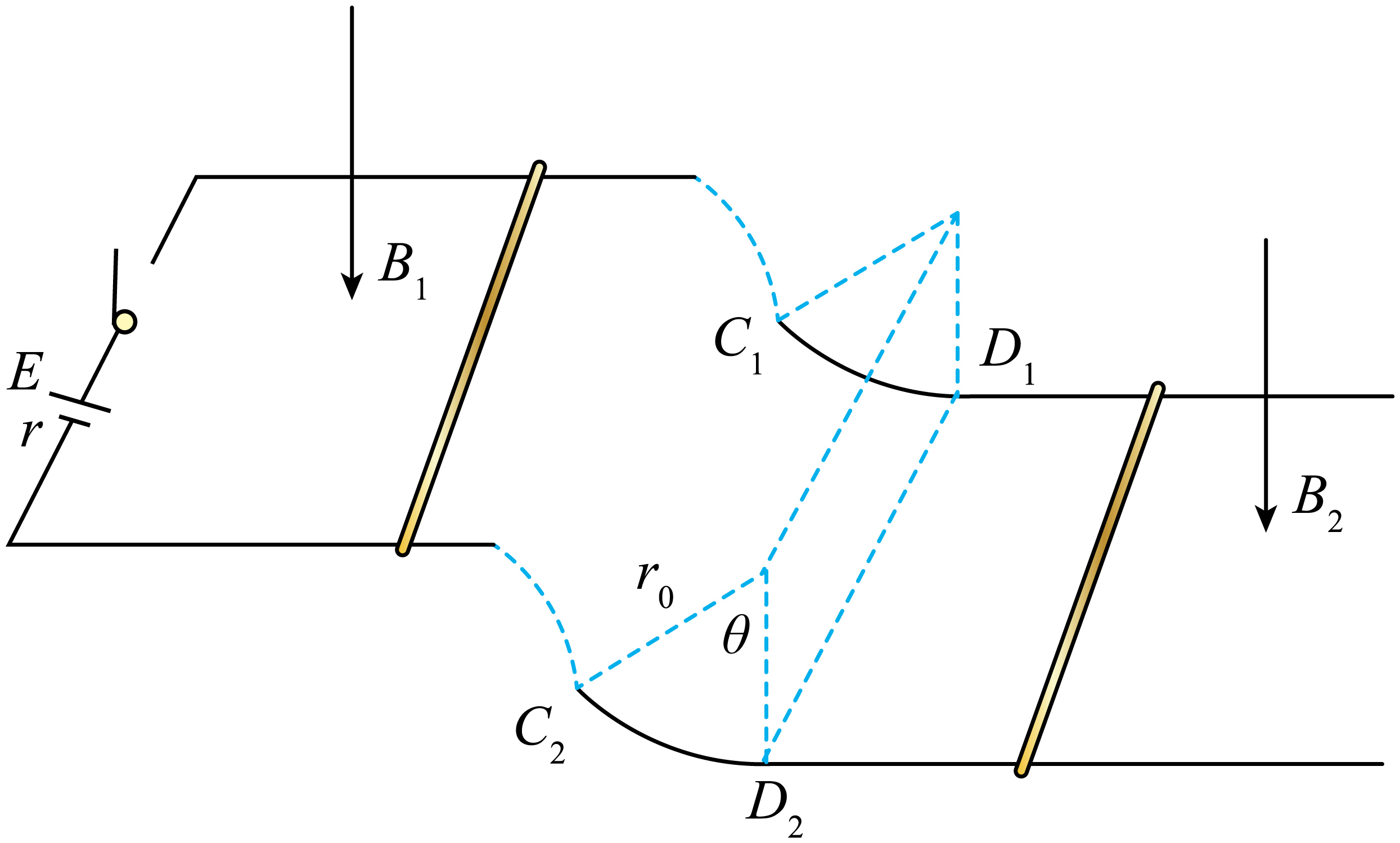
求闭合开关瞬间通过金属棒的电流$I$以及金属棒达到的最大速度$v_{1}$；

$1.2\\;\\rm A$，$1.6\\;\\rm m/s$；

由题意，根据闭合电路欧姆定律，可得闭合开关瞬间通过金属棒的电流$I=\dfrac{E}{r+R}=1.2\;\rm A$

闭合开关$\rm S$后金属棒在水平导轨上向右运动至速度稳定时，金属棒能以最大速度从上方轨道水平抛出，此时有$E=B_{1}Lv_{1}$

代入数据求得金属棒达到的最大速度$v_{1}=1.6\;\rm m/s$；

求金属棒从开始运动到获得最大速度过程中，通过金属棒的电荷量$q$；

$\\dfrac{8}{15}\\;\\rm C$；

金属棒从开始运动到获得最大速度过程中，根据动量定理有$F_{安}t=B_{1}ILt=B_{1}qL=mv_{1} − 0$

代入数据求得通过金属棒的电荷量$q=\dfrac{8}{15}\;\rm C$；

下方水平导轨区域内存在竖直向下的匀强磁场，磁感应强度$B_{2}=3\;\rm T$。导轨上放置质量$m_{2}=0.5\;\rm kg$、电阻为$3R$、长度为$L$的另一金属棒。若要使两金属棒在运动过程中恰好不发生碰撞，求金属棒$m_{2}$最终的速度和$m_{1}$刚到达$D_{1}D_{2}$时两金属棒之间的距离。

$1.5\\;\\rm m/s$，$0.8\\;\\rm m$。

闭合开关后，金属棒能以最大速度从上方轨道水平抛出，恰能从$C_{1}C_{2}$处沿切线进入圆弧轨道，根据平抛运动规律，可得金属棒$m_{1}$到达$C_{1}C_{2}$处的速度大小为$v_{2}=\dfrac{v_{1}}{\cos 37^\circ}= 2\;\rm m/s$

根据机械能守恒定律可得金属棒$m_{1}$到达水平轨道时，有$\dfrac{1}{2}m_{1}v_{2}^{2}+m_{1}gr_{0}(1-\cos 37^\circ)=\dfrac{1}{2}m_{1}v_{3}^{2}$

求得$v_{3}=3\;\rm m/s$

当金属棒$m_{1}$追上$m_{2}$时二者速度恰好相同，两金属棒在运动过程中恰好不发生碰撞，根据动量守恒定律有$m_{1}v_{3}=(m_{1}+m_{2})v_{4}$

求得金属棒$m_{2}$最终的速度$v_{4}=1.5\;\rm m/s$

对金属棒$m_{2}$利用动量定理有$B_{2}I'L\Delta t=m_{2}v_{4} − 0$，$I'\Delta t=q'=\dfrac{B_{2}L\Delta x}{R+3R}$

联立即可求得$m_{1}$刚到达$D_{1}D_{2}$时两金属棒之间的距离为$\Delta x=0.8\;\rm m$。