如图所示，一端固定的长为$l$的绝缘轻绳悬挂一质量为$m$的绝缘小球，小球带正电$q$，可视为质点。初始时，小球静止于$P$点，现给空间施加一大小为$E=\dfrac{\sqrt{3}mg}{3q}$，水平向右的恒定匀强电场，小球恰能到达$Q$点（未画出），已知重力加速度为$g$，不计空气阻力，则$(\quad\ \ \ \ )$

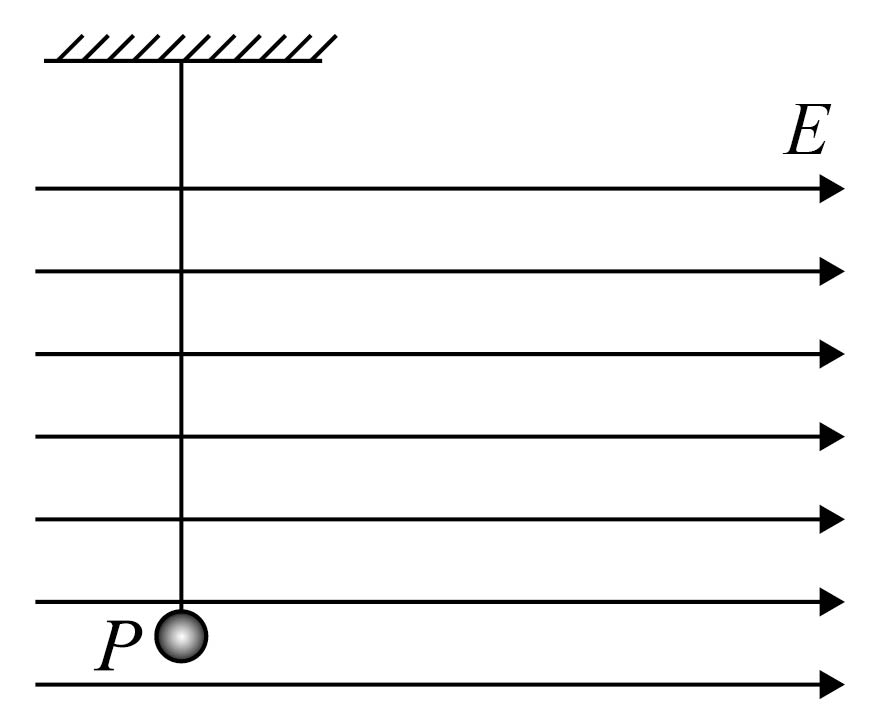
小球处于$Q$点位置时轻绳与竖直方向的夹角为$45{}^\\circ $

$P$、$Q$两点的电势差大小为$\\dfrac{mgl}{2q}$

轻绳对小球的拉力最大时，小球的电势能减少$\\dfrac{mgl}{6}$

轻绳对小球的拉力最大时，绳上的拉力大小为$\\dfrac{2\\sqrt{3}mg}{3}$

$\rm A$．题意可知小球恰能到达$Q$点时速度为$0$，设此时轻绳与竖直方向夹角为$\theta $，由动能定理有$Eql\text{sin}\theta -mgl\left( 1-\text{cos}\theta \right)=0$，代入数据，解得$\theta =60{}^\circ $，故$\rm A$错误；

$\rm B$．由场强与电势间的关系得：$U=El\sin\theta=\dfrac{mgl}{2q}$，故$\rm B$正确；

$\rm C$．轻绳对小球的拉力最大时，小球速度最大，由对称性得，此时轻绳与竖直方向夹角为$\dfrac{\theta }{2}$，该过程电场力做功$W=Eql\text{sin}30{}^\circ =\dfrac{\sqrt{3}mgl}{6}$，故小球的电势能减少$\dfrac{\sqrt{3}mgl}{6}$，故$\rm C$错误；

$\rm D$．小球速度最大时，由动能定理有$Eql\text{sin}\dfrac{\theta }{2}-mgl\left( 1-\text{cos}\dfrac{\theta }{2} \right)=\dfrac{1}{2}m{{v}^{2}}$，由牛顿第二定律有$F-\sqrt{{{\left( mg \right)}^{2}}+{{\left( Eq \right)}^{2}}}=m\dfrac{{{v}^{2}}}{l}$，联立解得$F=2\left( \sqrt{3}-1 \right)mg$

故$\rm D$错误。

故选$\rm B$。