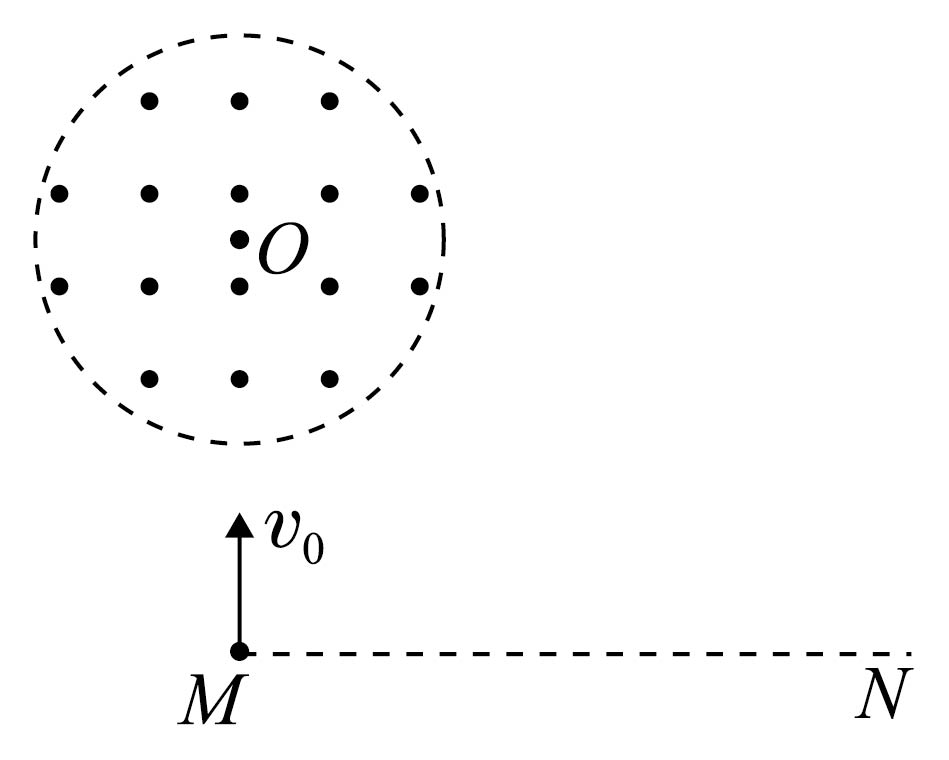
求匀强磁场的磁感应强度的大小$B$；

$B=\\dfrac{m{{v}_{0}}}{qR}$

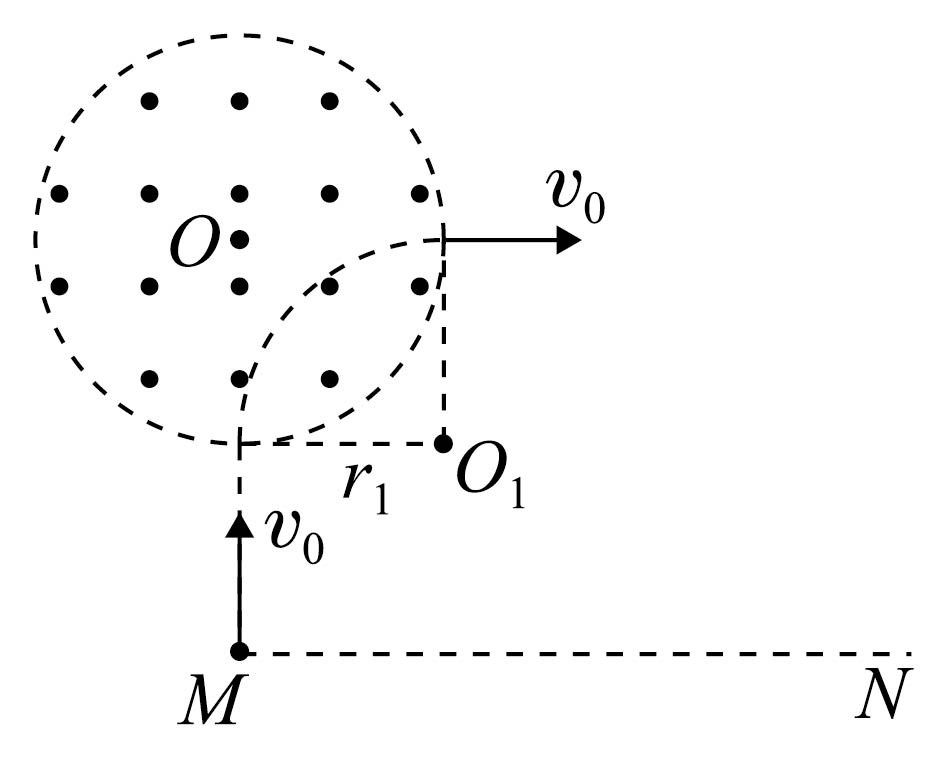
设粒子在磁场中的轨迹半径为${{r}_{1}}$，运动轨迹如图所示，由几何关系可知${{r}_{1}}=R$    

洛伦兹力提供向心力$q{{v}_{0}}B=m\dfrac{v_{0}^{2}}{{{r}_{1}}}$，解得$B=\dfrac{m{{v}_{0}}}{qR}$    

若该粒子以初速度$\dfrac{\sqrt{3}}{3}{{v}_{0}}$从$M$点沿垂直于$MN$向上的方向射出，求粒子从射出到返回虚线$MN$上所用的时间$t$。

$t=\\left( 4\\sqrt{3}+\\dfrac{2}{3}\\pi \\right)\\dfrac{R}{{{v}_{0}}}$

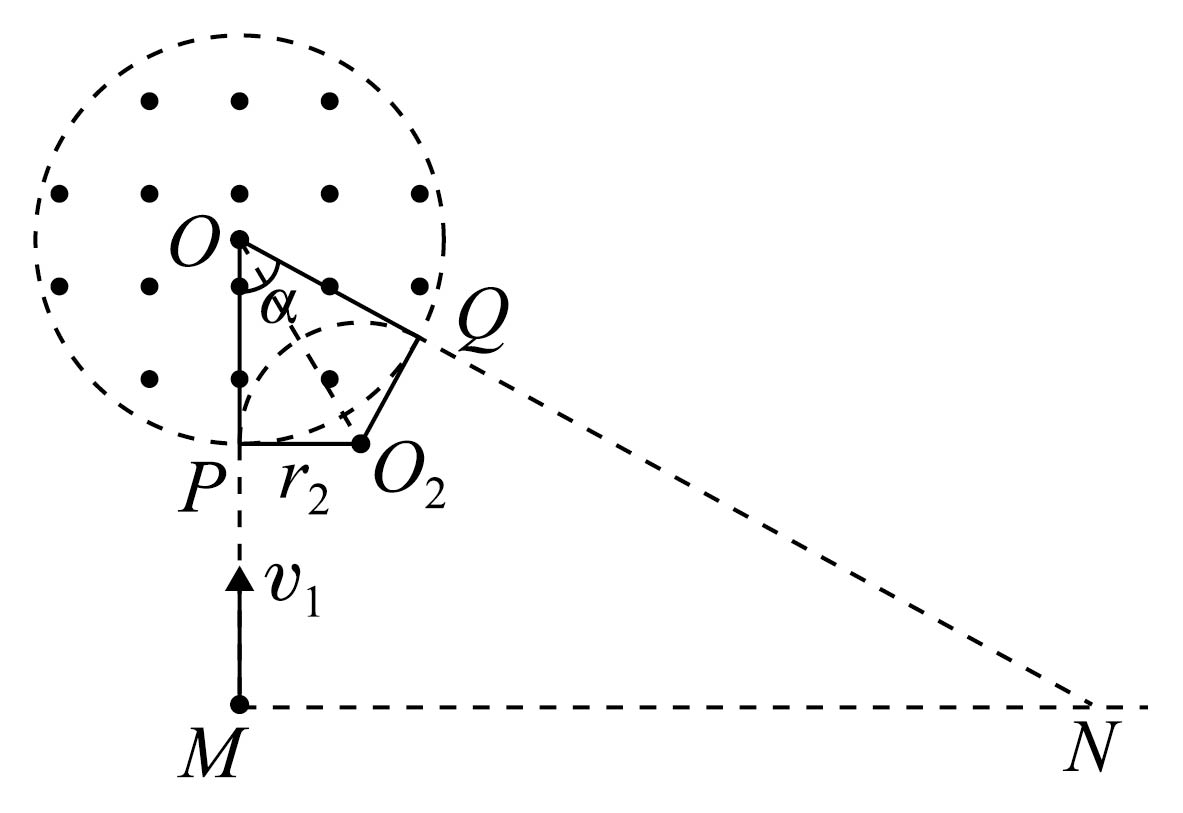
粒子以初速度${{v}_{1}}=\dfrac{\sqrt{3}}{3}{{v}_{0}}$进入磁场，运动轨迹如图所示，由$P$点射入磁场从$Q$点射出磁场，轨迹圆圆心为${{O}_{2}}$，设粒子在磁场中的轨迹圆半径为${{r}_{2}}$，运动的时间为${{t}_{1}}$；粒子在无磁场区域运动的总时间为${{t}_{2}}$

洛伦兹力提供向心力$q{{v}_{1}}B=m\dfrac{v_{1}^{2}}{{{r}_{2}}}$，解得${{r}_{2}}=\dfrac{\sqrt{3}}{3}R$    

由几何关系可知$\text{tan}\dfrac{\alpha }{2}=\dfrac{{{r}_{2}}}{R}$，$\angle POQ=\alpha =\dfrac{\pi }{3}$    

粒子在磁场中的运动时间为${{t}_{1}}=\dfrac{\left( \pi -\alpha \right){{r}_{2}}}{{{v}_{1}}}=\dfrac{2\pi R}{3{{v}_{0}}}$    

粒子在无磁场区域运动的总时间为$t_{2}=\dfrac{R+\left( \dfrac{2R}{\text{cos}\alpha}-R\right)}{v_{1}}=\dfrac{4\sqrt{3}R}{v_{0}}$    

粒子从$M$射出到返回虚线$MN$上所用的时间为$t={{t}_{1}}+{{t}_{2}}=\left( 4\sqrt{3}+\dfrac{2}{3}\pi \right)\dfrac{R}{{{v}_{0}}}$