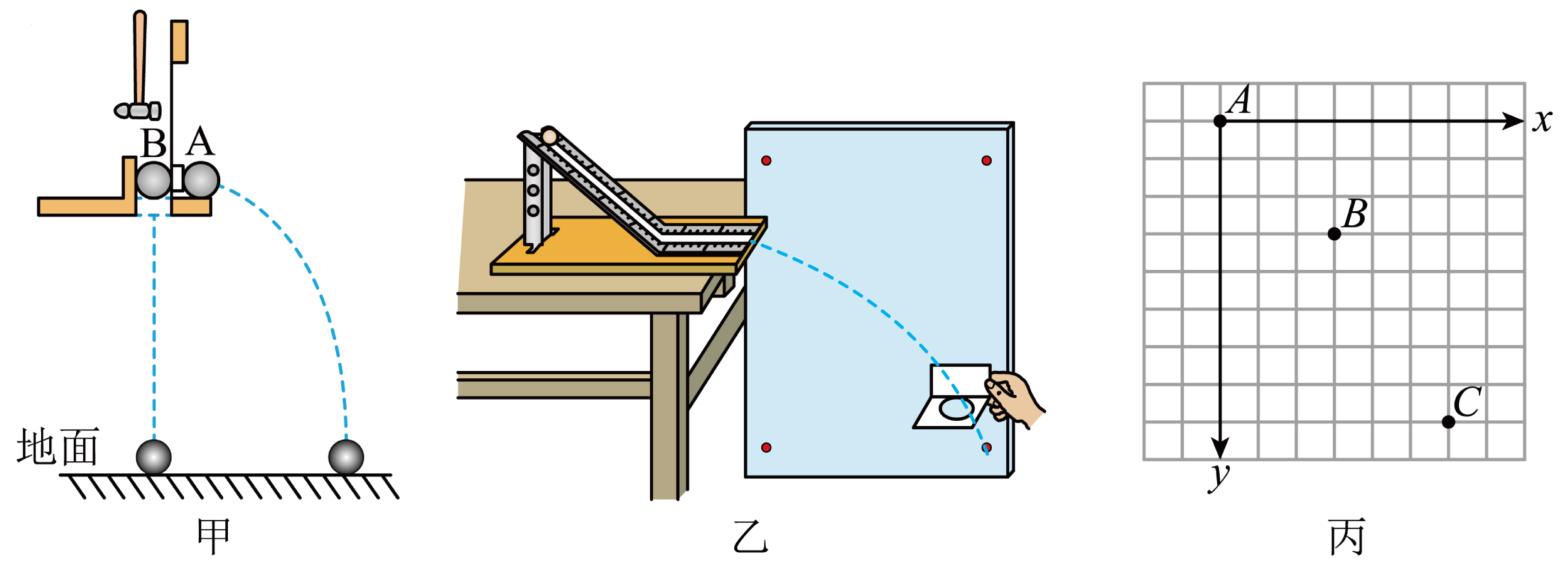
甲实验的现象是小球$A$、$B$同时落地，说明                 ；

甲实验时，小球$A$做平抛运动，小球$B$做自由落体运动，则实验现象是小球$A$、$B$同时落地，说明小球$A$在竖直方向的分运动是自由落体运动。

现将$A$、$B$球恢复初始状态后，用比较大的力敲击弹性金属片，$A$球落地点变远，则在空中运动的时间                 （填“变大”、“不变”或“变小”）；

将$A$、$B$球恢复初始状态后，用比较大的力敲击弹性金属片，$A$球落地点变远，可下落的高度不变， 由自由落体运动下落时间$t= \sqrt{\dfrac{2h}{g}}$可知，则在空中运动的时间不变。

安装图乙研究平抛运动实验装置时，保证斜槽末端水平，斜槽                 （填“需要”或“不需要”）光滑；

安装图乙研究平抛运动实验装置时，保证斜槽末端水平，使小球每次都做平抛运动，由于小球每次都是从斜槽上同一位置开始释放，小球在轨道上运动时克服阻力做功都相同，因此斜槽不需要光滑。

然后小明用图乙所示方法记录平抛运动的轨迹，由于没有记录抛出点，如图丙所示，数据处理时选择$A$点为坐标原点$(0,0)$，丙图中小方格的边长均为$20\;\rm cm$，重力加速度$g$取$10\;\rm m/s^{2}$，则小球平抛初速度的大小为                 $\;\rm m/s$，小球在$B$点速度的大小为                 $\;\rm m/s$。

由题图丙可知，两计数点间，小球在水平方向的位移相等，可知两计数点间的时间间隔相等，小球在竖直方向做自由落体运动，因此由匀变速直线运动的推论$\Delta y=gT^{2}$可得$T=\sqrt{\dfrac{\Delta y}{g}}=\sqrt{\dfrac{(5-3) \times 20 \times 10^{- 2}}{10}}\;\text{s}=0.2\;\rm \text{s}$

则小球平抛初速度的大小为$v_{0}=\dfrac{\Delta x}{T}=\dfrac{3 \times 20 \times 10^{- 2}}{0.2}\;{\text{m}}/{\text{s}}=3\;{\text{m}}/{\text{s}}$

小球在$y$轴方向由匀变速直线运动在某段时间内中间时刻的瞬时速度等于这段时间内的平均速度，可得小球在$B$点$y$轴方向速度的大小为$v_{y}=\dfrac{y_{AC}}{2T}=\dfrac{8 \times 20 \times 10^{- 2}}{2 \times 0.2}\;{\text{m}}/{\text{s}}=4\;{\text{m}}/{\text{s}}$

小球在$B$点速度的大小为$v_{B}=\sqrt{v_{0}^{2}+v_{y}^{2}}=\sqrt{3^{2}+4^{2}}\;{\text{m}}/{\text{s}}=5\;{\text{m}}/{\text{s}}$