| 机械能守恒定律 题目答案及解析
稿件来源:高途
| 机械能守恒定律题目答案及解析如下,仅供参考!
必修2
第七章 机械能守恒定律
7.8 机械能守恒定律
机械能守恒定律
如图所示,粗糙的水平面上有一半圆形凹槽,凹槽的质量为$M$,半圆弧的圆心为$O$点,最低点为$A$点,半径为$R$。现将一质量为$m$的光滑小球从圆弧上的$D$点由静止释放,已知$OD$与$OA$的夹角为$\theta(\theta\lt 5^\circ)$,重力加速度为$g$,小球大小可以忽略不计,从$D$点运动到$A$点的过程中,凹槽始终保持静止。下列说法正确的是$(\qquad)$
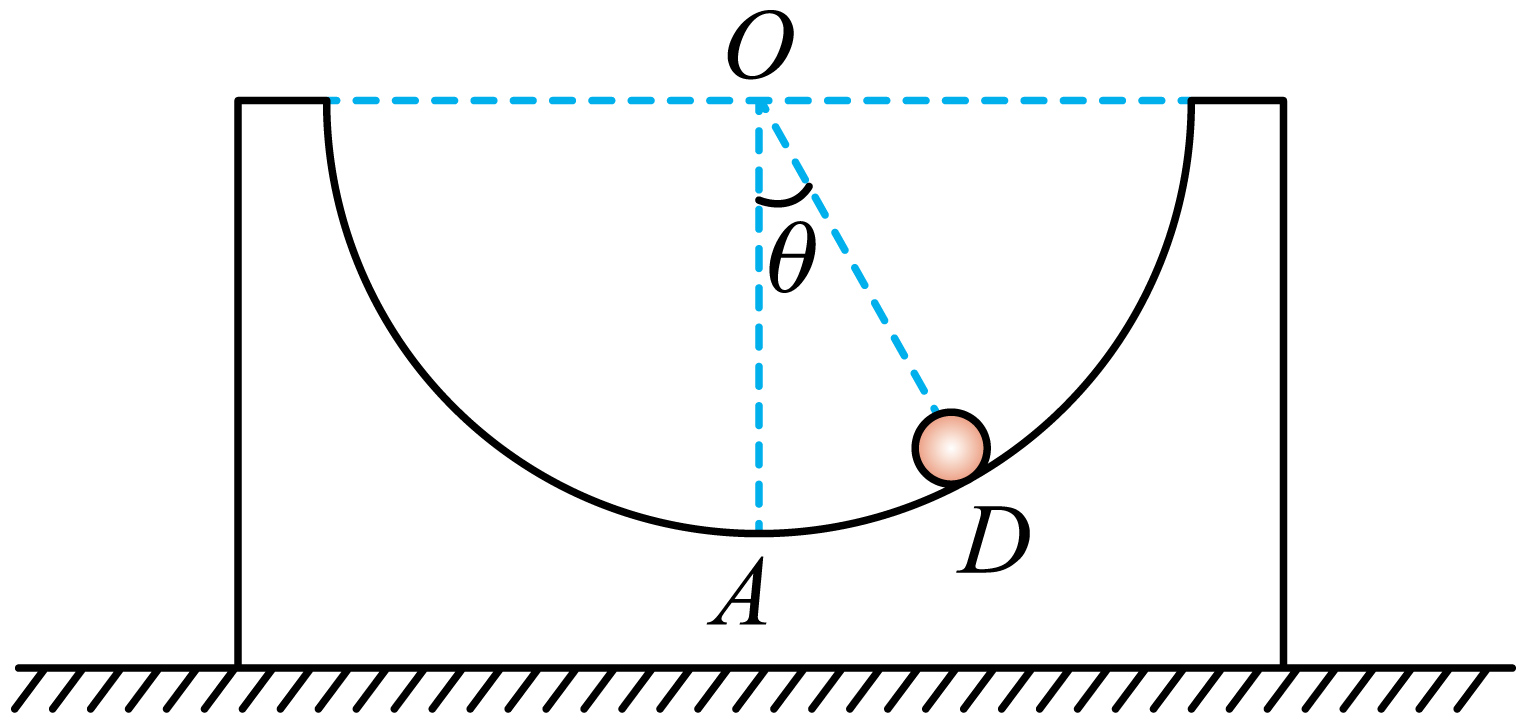
小球从$D$点运动到$A$点过程中,小球和凹槽所组成的系统,机械能守恒,动量也守恒
","小球到达$A$点时对凹槽的压力大小为$3mg-2mg\\cos\\theta$
","小球从$D$点运动到$A$点的时间为$t=\\dfrac{\\pi}{2}\\sqrt{\\dfrac{R}{g}}$
","小球从$D$点运动到$A$点过程中,水平面摩擦力对凹槽的冲量大小为$m\\sqrt{2gR(1-\\cos\\theta)}$
"]$\rm A$.小球和凹槽所组成的系统,在该过程中,由于地面有静摩擦力,但静摩擦未做功,机械能守恒,动量不守恒,故$\rm A$错误;
$\rm B$.小球从$D$点到$A$点,由机械能守恒定律可得$mgR(1-\cos\theta)=\dfrac{1}{2}mv^{2}$
在$A$点有$F_{\text{N}}-mg=m\dfrac{v^{2}}{R}$
解得$v=\sqrt{2gR(1-\cos\theta)}$
$F_{\rm N}=3mg-2mg\cos \theta$
故$\rm B$正确;
$\rm C$.由单摆的周期可知,小球从$D$点运动到$A$点的时间为$t=\dfrac{1}{4}T=\dfrac{\pi}{2}\sqrt{\dfrac{R}{g}}$
故$\rm C$正确;
$\rm D$.凹槽始终静止,水平面摩擦力对凹槽的冲量与小球对凹槽的水平冲量等大反向,由动量定理可知$I_{\text{f}}=I_{弹}=m\Delta v=m\sqrt{2gR(1-\cos\theta)}$
故$\rm D$正确。
故选:$\rm BCD$。
| 机械能守恒定律题目答案及解析(完整版)
