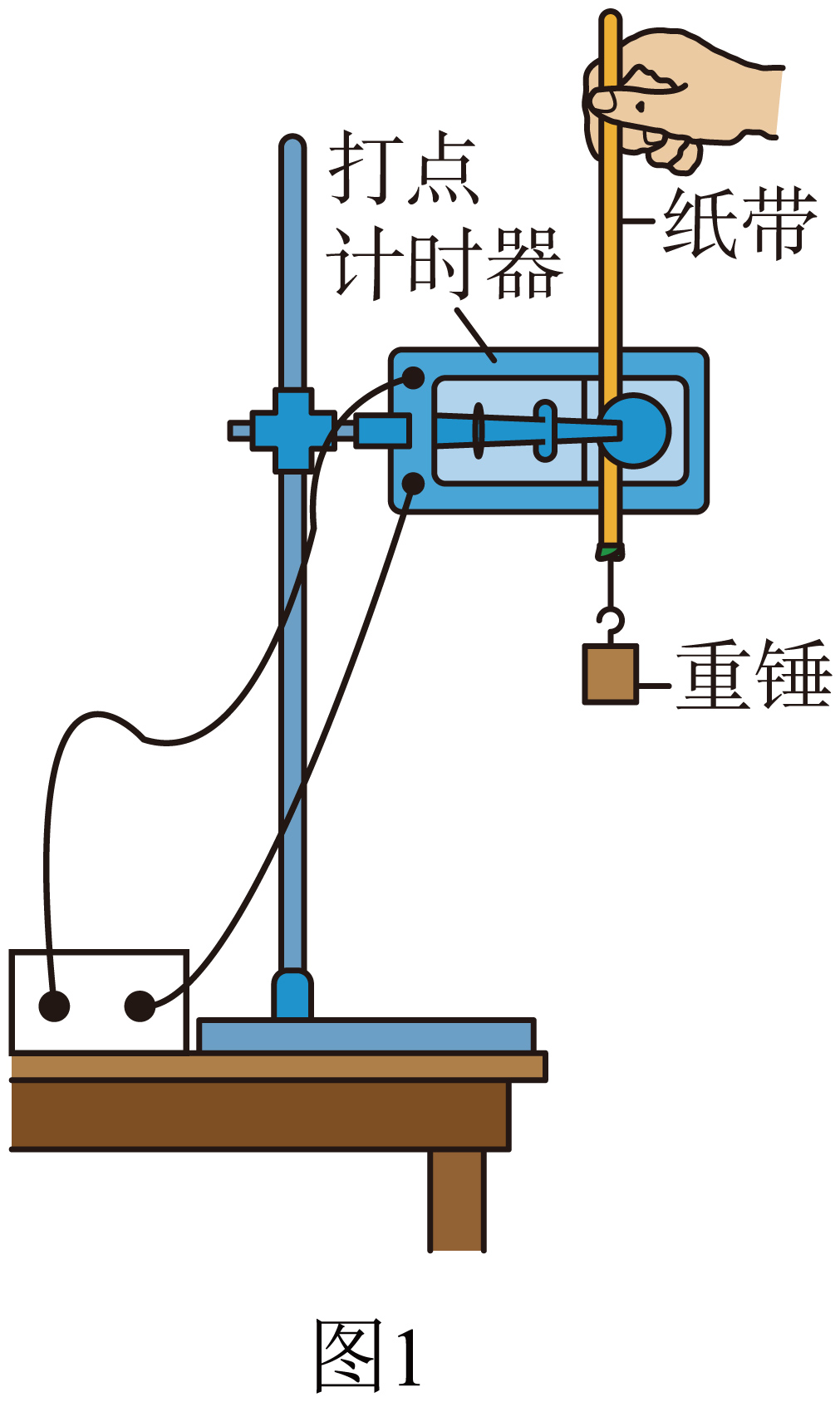
下列所给实验步骤中，有$4$个是完成实验必需且正确的，把它们选择出来并按实验顺序排列：                 （填步骤前面的序号）

①先接通电源，打点计时器开始打点，然后再释放纸带

②先释放纸带，然后再接通电源，打点计时器开始打点

③用电子天平称量重锤的质量

④将纸带下端固定在重锤上，穿过打点计时器的限位孔，用手捏住纸带上端

⑤在纸带上选取一段，用刻度尺测量该段内各点到起点的距离，记录分析数据

⑥关闭电源，取下纸带

实验步骤为：将纸带下端固定在重锤上，穿过打点计时器的限位孔，用手捏住纸带上端，先接通电源，打点计时器开始打点，然后再释放纸带，关闭电源，取下纸带，在纸带上选取一段，用刻度尺测量该段内各点到起点的距离，记录分析数据，根据原理$mgh= \dfrac{1}{2}mv^{2}$可知质量可以约掉，不需要用电子天平称量重锤的质量。

故选正确且正确排序为④①⑥⑤。

图$2$所示是纸带上连续打出的五个点$A$、$B$、$C$、$D$、$E$到起点的距离。则打出$B$点时重锤下落的速度大小为                  $\rm m/s$（保留$3$位有效数字）。

根据题意可知纸带上相邻计数点时间间隔$T =\dfrac{1}{f}=0.02\;\rm \text{s}$

根据匀变速直线运动中间时刻瞬时速度等于该过程平均速度可得$v_{B}=\dfrac{h_{AC}}{2T}$

代入数据可得$v_{B}\approx 1.79\;\rm m/s$

纸带上各点与起点间的距离即为重锤下落高度$h$，计算相应的重锤下落速度$v$，并绘制图$3$所示的$v^{2}-h$关系图像。理论上，若机械能守恒，图中直线应                 （填“通过”或“不通过”）原点且斜率为                 （用重力加速度大小$g$表示）。由图$3$得直线的斜率$k=$                 （保留$3$位有效数字）。

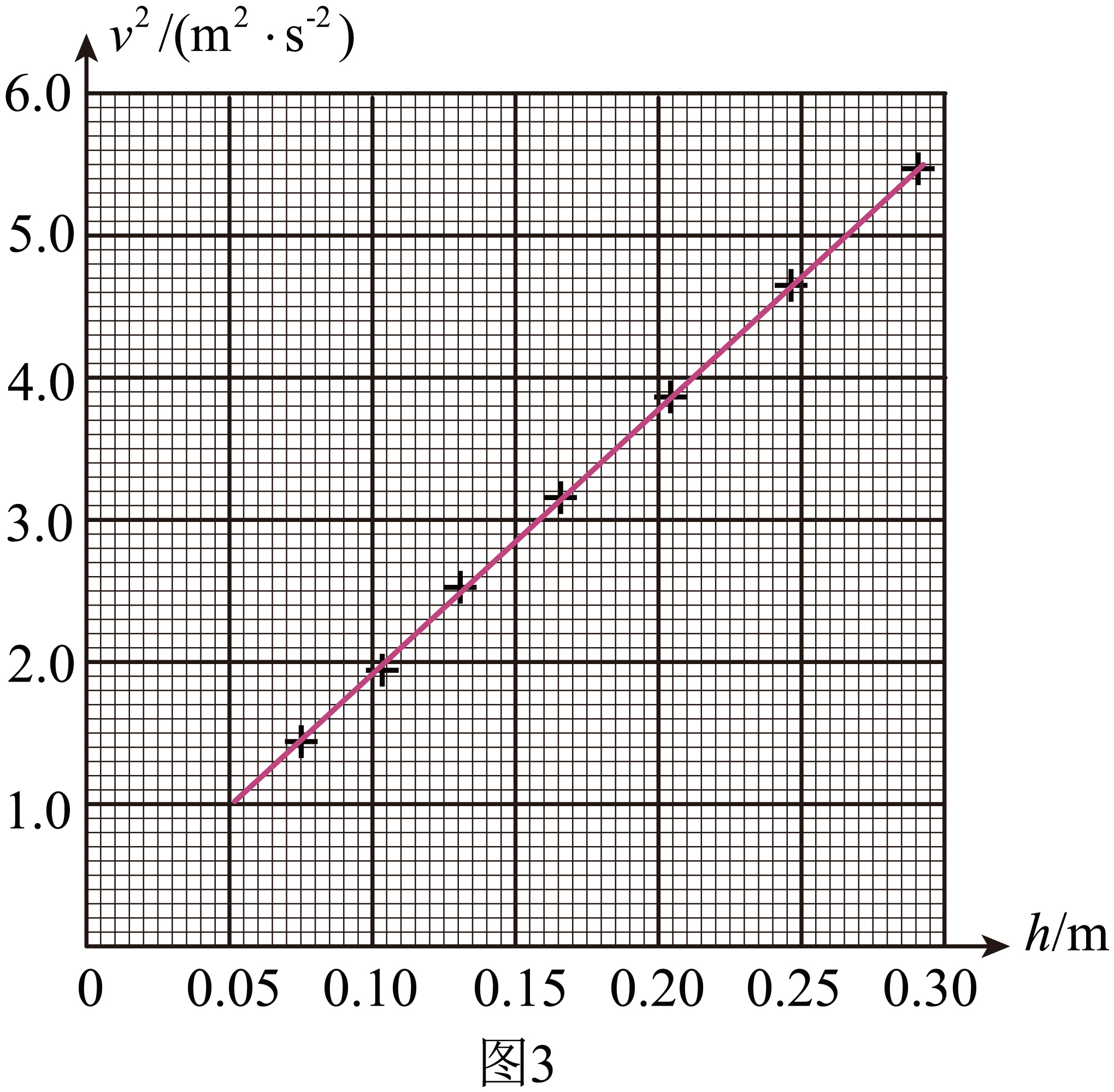
根据$mgh= \dfrac{1}{2}mv^{2}$

整理可得$v^{2}=2g ⋅ h$

可知理论上，若机械能守恒，图中直线应通过原点，且斜率$k=2g$

由图$3$得直线的斜率$k=\dfrac{5.6-1.5}{0.295-0.08} \approx 19.0$

定义单次测量的相对误差$\eta=\left| \dfrac{E_{\text{p}}-E_{\text{k}}}{E_{\text{p}}} \right| \times 100\%$，其中$E_{\rm p}$是重锤重力势能的减小量，$E_{\rm k}$是其动能增加量，则实验相对误差为$\eta=$                 $\times 100\%$（用字母$k$和$g$表示）；当地重力加速度大小取$g=9.80\;\rm m/s^{2}$，则$\eta=$                 $\%$（保留$2$位有效数字），若$\eta\lt 5\%$，可认为在实验误差允许的范围内机械能守恒。

根据题意有$\eta=\dfrac{mgh- \dfrac{1}{2}mv^{2}}{mgh} \times 100\%$

可得$\eta=\dfrac{2g-k}{2g} \times 100\%$

当地重力加速度大小取$g=9.80\;\rm m/s^{2}$，代入数据可得$\eta\approx 3.1\%$。