| 闭合电路的欧姆定律基本问题 题目答案及解析
稿件来源:高途
| 闭合电路的欧姆定律基本问题题目答案及解析如下,仅供参考!
选修3-1
第二章 恒定电流
2.7 闭合电路的欧姆定律
闭合电路的欧姆定律基本问题
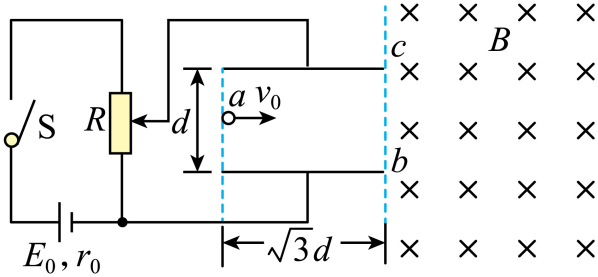
如图。直流电源的电动势为$E_{0}$,内阻为$r_{0}$,滑动变阻器$R$的最大阻值为$2r_{0}$,平行板电容器两极板水平放置,板间距离为$d$,板长为$\sqrt{3}d$,平行板电容器的右侧存在方向垂直纸面向里的匀强磁场。闭合开关$\rm S$,当滑片处于滑动变阻器中点时,质量为$m$的带正电粒子以初速度$v_{0}$水平向右从电容器左侧中点$a$进入电容器,恰好从电容器下极板右侧边缘$b$点进入磁场,随后又从电容器上极板右侧边缘$c$点进入电容器,忽略粒子重力和空气阻力。
求粒子所带电荷量$q$;
$q= \\dfrac{mv_{0}^{2}}{E_{0}}$;
"]]粒子在电容器中做类平抛运动,水平方向做匀速直线运动有$\sqrt{3}d=v_{0}t$
竖直方向做匀变速直线运动$\dfrac{d}{2}=\dfrac{0+v_{y}}{2}t$,$v_{y}=at=\dfrac{qU}{md}t$
由闭合回路欧姆定律可得$U=\dfrac{r_{0}}{r_{0}+2r_{0}}E$
联立可得$v_{y}=\dfrac{\sqrt{3}}{3}v_{0}$,$q=\dfrac{mv_{0}^{2}}{E_{0}}$;
求磁感应强度$B$的大小;
$B=\\dfrac{2E_{0}}{dv_{0}}$;
"]]粒子进入磁场与竖直方向的夹角为$\tan\theta=\dfrac{v_{x}}{v_{y}}= 60{^\circ}$,$v=\dfrac{v_{0}}{\sin 60{^\circ}}=\dfrac{2\sqrt{3}}{3}v_{0}$
粒子在磁场中做匀速圆周运动$qvB=m\dfrac{v^{2}}{R}$
由几何关系易得$R=\dfrac{d}{\cos 30{^\circ}}=\dfrac{\sqrt{3}d}{3}$
联立可得$B=\dfrac{2E_{0}}{dv_{0}}$;
若粒子离开$b$点时,在平行板电容器的右侧再加一个方向水平向右的匀强电场,场强大小为$\dfrac{4\sqrt{3}E_{0}}{3d}$,求粒子相对于电容器右侧的最远水平距离$x_\rm{m}$。
$\\dfrac{\\left( 2+\\sqrt{3} \\right)d}{2}$。
"]]取一个竖直向上的速度使得其对应的洛伦兹力和水平向右的电场力平衡,则有$qv_{y1}B=qE$
解得$v_{y1}=\dfrac{2\sqrt{3}}{3}v_{0}$
粒子以$v_{y1}$速度向上做匀速直线运动,粒子做圆周运动的合速度的竖直方向分速度为$v_{y2}=v_{y1}+v_{y}=\sqrt{3}v_{0}$
此时合速度与竖直方向的夹角为$\tan\alpha=\dfrac{v_{0}}{\sqrt{3}v_{0}}$
合速度为$v'=\sqrt{\left( \sqrt{3}v_{0} \right)^{2}+v_{0}^{2}}$
粒子做圆周运动的半径$r=\dfrac{mv'}{Bq}$
最远距离为$x_{m}=r+r\cos\alpha=\dfrac{\left( 2+\sqrt{3} \right)d}{2}$。
| 闭合电路的欧姆定律基本问题题目答案及解析(完整版)
