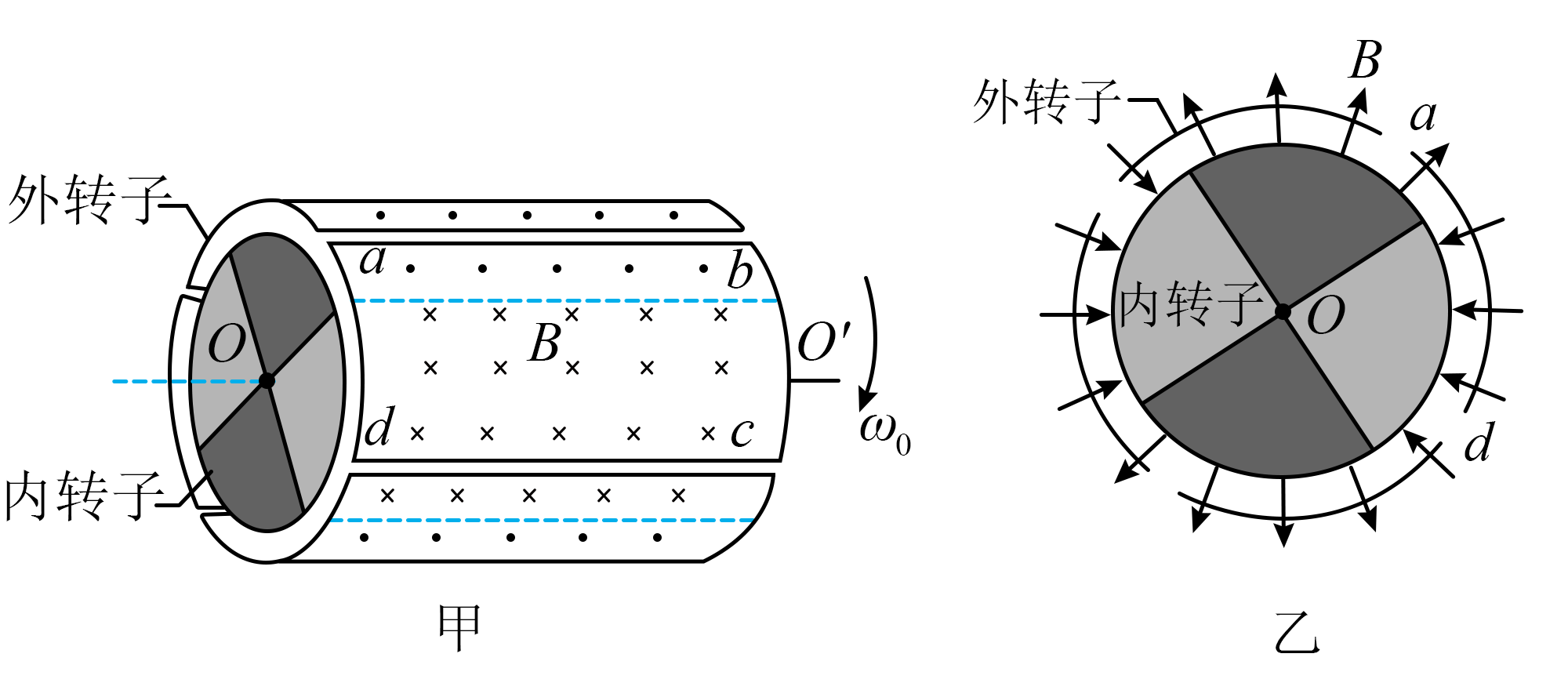
若内转子固定，求$ab$边产生感应电动势的大小$E$；

$BL\\omega_{0}r_{1}$；

根据题意可知，$ab$转动时的线速度为$v=\omega_{0}r_{1}$

则$ab$产生的感应电动势$E_{1}=BLv=BL\omega_{0}r_{1}$；

若内转子固定，求外转子转动一周，线圈$abcd$产生的焦耳热$Q$；

$\\dfrac{8\\pi B^{2}L^{2}\\omega_{0}r_{1}^{2}}{R}$；

根据题意，由图可知，若内转子固定，外转子转动过程中，$ab$、$cd$均切割磁感线，且产生的感应电流方向相反，则转动过程中感应电动势为$E_{2}=2BLv=2BL\omega_{0}r_{1}$

感应电流为$I=\dfrac{E_{2}}{R}$

转子转动的周期为$T=\dfrac{2\pi}{\omega_{0}}$

则$abcd$转一圈产生的热量$Q=I^{2}RT=\dfrac{8\pi B^{2}L^{2}r_{1}^{2}\omega_{0}}{R}$；

若内转子不固定，外转子带动内转子匀速转动，此时线圈中感应电流为$I$，求线圈$abcd$中电流的周期$T$。

$\\dfrac{2\\pi BLr_{1}}{IR}$。

结合图可知，转子转动$\dfrac{1}{4}T$电流方向改变，大小不变，若内转子不固定，跟着外转子一起转，且$abcd$中的电流为$I$，则感应电动势为$E'=IR$

又有$E'=2BL\Delta v$

解得$\Delta v=\dfrac{IR}{2BL}$

则电流改变方向的时间为$t=\dfrac{\dfrac{1}{4} \times 2\pi r_{1}}{\Delta v}=\dfrac{BL\pi r_{1}}{IR}$

则电流的周期为$T=2t=\dfrac{2BL\pi r_{1}}{IR}$。