如图，下列元件在匀强磁场中绕中心轴转动，下列电动势最大的是$(\quad\ \ \ \ )$

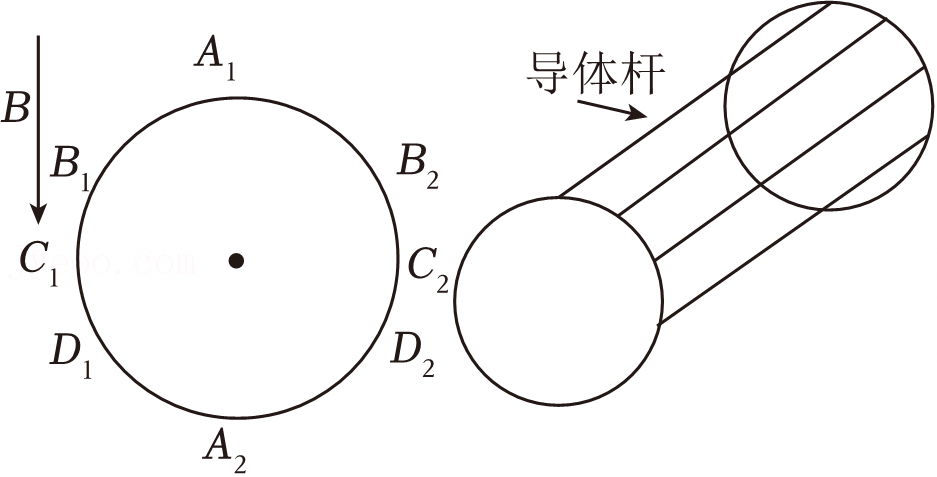
$A_{1}$和$A_{2}$

$B_{1}$和$B_{2}$

$C_{1}$和$C_{2}$

$D_{1}$和$D_{2}$

由图可知，磁场方向竖直向下，图中各点的线速度都沿切线方向，而此时$A_{1}$和$A_{2}$点速度方向与磁场方向垂直，产生的感应电动势最大。故$\rm BCD$错误，$\rm A$正确；

故选：$\rm A$；

在倾斜角为$4.8^\circ$的斜坡上，有一辆向下滑动的小车在做匀速直线运动，存在动能回收系统；小车的质量$m=1500\;\rm kg$。在$t=5\;\rm s$时间内，速度从$v_{0}=72\;\rm km/h$减速到$v_{t}=18\;\rm km/h$，运动过程中所有其他阻力的合力$f=500\;\rm N$。求这一过程中：

①小车的位移大小$x$？

②回收作用力大小$F$？

①小车的位移大小$x$为$62.5\\;\\rm m$；②回收作用力大小$F$为$5230\\;\\rm N$

①小车的位移$x=\dfrac{v_{0}+ v_{t}}{2}t=\dfrac{20+5}{2} \times 5\;\rm m=62.5\;\rm m$

②小车的加速度$a=\dfrac{v_{t}-v_{0}}{t}=\dfrac{5-20}{5}\;\rm m/s^{2}=- 3\;\rm m/s^{2}$

方向沿斜面向上，根据牛顿第二定律$F+f-mg\sin4.8^{\circ}=ma$

解得$F=5230\;\rm N$；

如图，大气压强为$p_{0}$，一个气缸内部体积为$V_{0}$，初始压强为$p_{0}$，内有一活塞横截面积为$S$，质量为$M$。

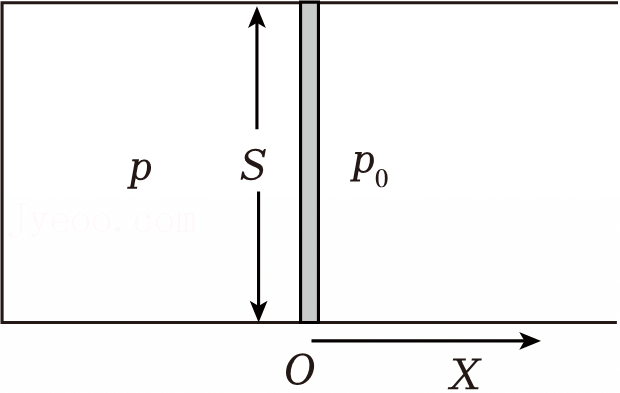
①等温情况下，向右拉开活塞移动距离$X$，求活塞受拉力$F$？

②在水平弹簧振子中，弹簧劲度系数为$k$，小球质量为$m$，则弹簧振子做简谐运动振动频率为$f=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m}}$，论证拉开微小位移$X$时，活塞做简谐振动，并求出振动频率$f$；

③若气缸绝热，活塞在该情况下振动频率为$f_{2}$，上题中等温情况下，活塞在气缸中的振动频率为$f_{1}$，则两则的大小关系为                 。

$\rm A$．$f_{1}\gt f_{2}$

$\rm B$．$f_{1}=f_{2}$

$\rm C$．$f_{1}\lt f_{2}$

①等温情况下，向右拉开活塞移动距离$X$，活塞受拉力$F$为$\\dfrac{p_{0}S^{2}X}{V_{0}+ SX}$；②拉开微小位移$X$时，活塞做简谐振动的证明见解析，振动频率$f$为$\\dfrac{1}{2\\pi}\\sqrt{\\dfrac{p_{0}S^{2}}{MV_{0}}}$；③$\\rm C$

①根据玻意耳定律$p_{0}V_{0}=p(V_{0}+XS)$

对活塞分析可知$F=(p_{0}﹣p)S$

解得$F=\dfrac{p_{0}S^{2}X}{V_{0}+SX}$

②设$X$方向为正方向，则此时活塞所受合力$F_{回}=- (p_{0}-p)S=- \dfrac{p_{0}S^{2}}{V_{0}+SX}X$

当$X$很微小时，则$F_{回} \approx-\dfrac{p_{0}S^{2}}{V_{0}}X=- kX$

即活塞的振动可视为简谐振动。其中$k=\dfrac{p_{0}S^{2}}{V_{0}}$

振动频率为$f=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{M}}=\dfrac{1}{2\pi}\sqrt{\dfrac{p_{0}S^{2}}{V_{0}M}}$

③若气缸绝热，则当气体体积增大时，气体对外做功，内能减小，温度降低，则压强减小，即$p'\lt p$，根据$f_{回}=- (p_{0}-p)s=- \dfrac{p_{0}s^{2}}{v_{0}+sx}x$，

则$k$值偏大，则$f_{1}\lt f_{2}$

故$\rm AB$错误，$\rm C$正确。

故选：$\rm C$。