| 动生电动势 题目答案及解析
稿件来源:高途
| 动生电动势题目答案及解析如下,仅供参考!
选修3-2
第四章 电磁感应
4.5 电磁感应现象的两类情况
动生电动势
如图所示,长度均为$s$的两根光滑金属直导轨$MN$和$PQ$固定在水平绝缘桌面上,两者平行且相距$l$,$M$、$P$连线垂直于导轨,定滑轮位于$N$、$Q$连线中点正上方$h$处。$MN$和$PQ$单位长度的电阻均为$r$,$M$、$P$间连接一阻值为$2sr$的电阻。空间有垂直于桌面向下的匀强磁场,磁感应强度大小为$B$。过定滑轮的不可伸长绝缘轻绳拉动质量为$m$、电阻不计的金属杆沿导轨向右做匀速直线运动,速度大小为$v$。零时刻,金属杆位于$M$、$P$连线处。金属杆在导轨上时与导轨始终垂直且接触良好,重力加速度大小为$g$。
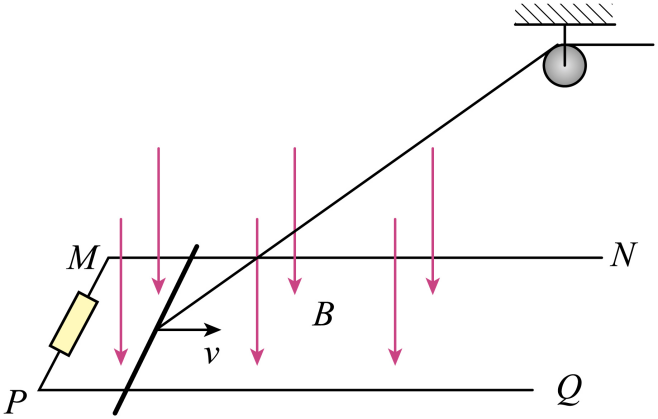
金属杆在导轨上运动时,回路的感应电动势;
$Blv$;
"]]金属杆在导轨上运动时,切割磁感线,产生感应电动势$E=Blv$;
金属杆在导轨上与$M$、$P$连线相距$d$时,回路的热功率;
$\\dfrac{B^{2}l^{2}v^{2}}{2r(d+ s)}$;
"]]金属杆运动距离$d$时,电路中的总电阻为$R=2dr+2sr$
故此时回路中的总的热功率为$P=\dfrac{E^{2}}{R}=\dfrac{B^{2}l^{2}v^{2}}{2r(d+s)}$;
金属杆在导轨上保持速度大小$v$做匀速直线运动的最大路程。
$\\sqrt{s^{2}- \\dfrac{B^{2}l^{2}hv}{2mgr}}$。
"]]设金属杆保持速度大小$v$做匀速直线运动的最大路程为$x$,此时刚好将要脱离导轨,此时绳子拉力为$T$,与水平方向的夹角为$\theta$ ,对金属杆根据受力平衡可知$F_{安}=T\cos \theta$,$mg=T\sin \theta$
根据位置关系有$\tan\theta=\dfrac{h}{s-x}$
同时有$F_{安}=BIl$,$I=\dfrac{Blv}{2r(x+s)}$
联立解得$x=\sqrt{s^{2}-\dfrac{B^{2}l^{2}hv}{2mgr}}$。
| 动生电动势题目答案及解析(完整版)
