当$\alpha=45^\circ $时，求光线从$AB$边射入棱镜时折射角的正弦值；

$\\dfrac{\\sqrt{6}}{4}$

作出光路图，如图所示

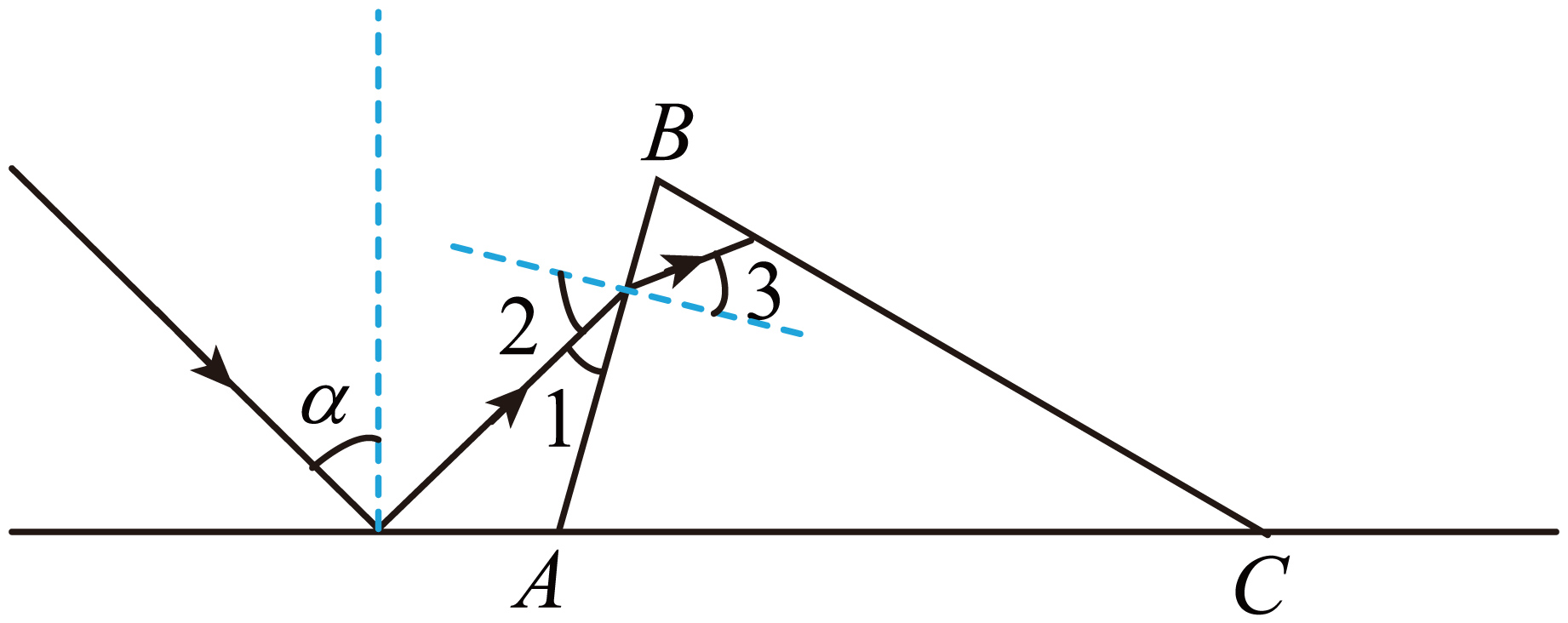
由几何关系可知$\angle BAC=\dfrac{180{^\circ}-\angle C}{2}=75{^\circ}$，$∠1=∠BAC-(90^\circ-\alpha)=30^\circ $

所以在$AB$边的入射角为$∠2=90^\circ-∠1=60^\circ $

由光的折射定律$n=\dfrac{\sin\angle 2}{\sin\angle 3}$

解得光线从$AB$边射入棱镜时折射角的正弦值为$\sin\angle 3=\dfrac{\sqrt{6}}{4}$

若光线从$AB$边折射后直接到达$BC$边，并在$BC$边刚好发生全反射，求此时的$\alpha$值

$60^\\circ $

根据$\sin C'=\dfrac{1}{n}= \dfrac{\sqrt{2}}{2}$

可得$C'=45^\circ $

则$AB$边的折射角为$∠3'=90^\circ-[180^\circ-(75^\circ +90^\circ-45^\circ )]=30^\circ $

根据折射定律可知$AB$边的入射角满足$n=\dfrac{\sin\angle 2'}{\sin\angle 3'}$

解得$∠2'=45^\circ $

根据几何关系可知恰好发生全反射时的入射角为$\alpha'=90^\circ-[∠BAC-(90^\circ-∠2')]=60^\circ $