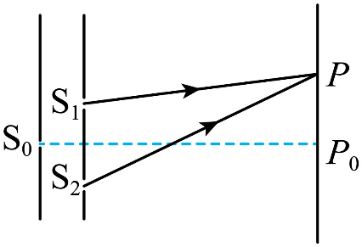
某一质检部门利用干涉原理测定矿泉水的折射率。如图所示，单缝$S_{0}$、屏上的$P_{0}$点位于双缝$S_{1}$和$S_{2}$的中垂线上，当双缝与屏之间的介质为空气或矿泉水时，屏上的干涉条纹间距分别为∆$x_{1}$与∆$x_{2.}$，当介质为矿泉水时，屏上$P$点处是$P_{0}$上方的第$4$条亮条纹（不包括$P_{0}$点处的亮条纹）的中心。已知入射光在真空中的波长为$\lambda$，真空中的光速为$c$，则$(\qquad)$

$\\Delta x_{2}$大于$\\Delta x_{1}$

该矿泉水的折射率为$\\dfrac{\\Delta x_{2}}{\\Delta x_{1}}$

当介质为矿泉水时，来自$S_{1}$和$S_{2}$的光传播到$P$点处的时间差为$\\dfrac{3\\lambda}{c}$

仅将$S_{0}$水平向左移动的过程中，$P$点仍能观察到亮条纹

$\rm A$．根据杨氏双缝干涉相邻条纹间距的公式有$\Delta x=\dfrac{L}{d}\lambda$，当双缝与屏之间的介质为矿泉水时，波长会变小，而双缝间距$d$与双缝与屏之间的距离$L$相同，所以∆$x_{2}$小于∆$x_{1}$，故$\rm A$错误；

$\rm B$．设光在真空中的波长为$\lambda$、在介质中的波长为$\lambda'$，依题意有$\Delta x_{1}=\dfrac{L}{d}\lambda$、$\Delta x_{2}=\dfrac{L}{d}\lambda'$、$\lambda'=\dfrac{\lambda}{n}$，则可知$\dfrac{\Delta x_{1}}{\Delta x_{2}}=n$，故$\rm B$错误；

$\rm C$．$P$点处是$P_{0}$上方的第$4$条亮条纹的中心，则光到双缝的光程差为光在矿泉水波长的$4$倍，则来自$S_{1}$和$S_{2}$的光传播到$P$点处的时间差为$t=\dfrac{4\lambda'}{\dfrac{c}{n}}=\dfrac{4\dfrac{\lambda}{n}}{\dfrac{c}{n}}=\dfrac{4\lambda}{c}$，故$\rm C$错误；

$\rm D$．将$S_{0}$水平向左移动的过程中，$P$点与双缝光程差不会改变，据题仍是光在介质中波长的四倍，所以仍能观察到亮条纹，故$\rm D$正确。

故选：$\rm D$。