某种喷墨打印机打印头的结构简图如图所示。其中喷盒可以喷出极小的墨汁微粒，此微粒经过带电室后以一定的初速度垂直射入偏转电场，再经偏转电场后打到纸上，显示出字符。忽略墨汁的重力，为了使打在纸上的字迹缩小，下列措施理论上可行的是$(\qquad)$

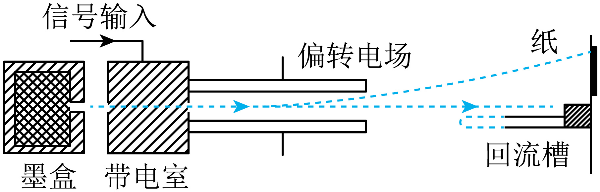
仅减小偏转电场的电压

仅增大墨汁微粒所带的电荷量

仅增大墨汁微粒的质量

仅增大墨汁微粒进入偏转电场的速度

设喷入偏转电场的墨汁微粒的速度为$v_{0}$，偏转电场两极板的长度为$L$，偏转电场右边缘与纸间距为$L'$，墨滴在$x$方向上匀速运动$L=v_{0}t$，根据牛顿第二定律可得$a=\dfrac{qU}{md}$，在竖直方向上做匀加速运动$y_{1}=\dfrac{1}{2}at^{2}=\dfrac{qUL^{2}}{2mdv_{0}^{2}}$，由几何关系得$\dfrac{y_{1}}{y_{2}}=\dfrac{\dfrac{L}{2}}{\dfrac{L}{2}+L^{'}}$，则墨汁在纸上竖直方向的偏移量$y_{2}=\left(1+\dfrac{2L'}{L}\right)\dfrac{qUL^{2}}{2mdv_{0}^{2}}$，根据表达式可知，为了使打在纸上的字迹缩小，即减小$y_{2}$，可减小墨汁微粒所带的电荷量，增大墨汁微粒的质量，减小偏转电场的电压，增大墨汁微粒的喷出速度。

故选：$\rm ACD$。