| 运动的合成与分解 题目答案及解析
稿件来源:高途
| 运动的合成与分解题目答案及解析如下,仅供参考!
必修2
第五章 曲线运动
5.1 曲线运动
运动的合成与分解
如图所示,光滑绝缘水平轨道$MS$上方的$NSOP$区域内有竖直向上的匀强电场,以$O$点为坐标原点建立坐标系,在第一象限中有垂直纸面向外的匀强磁场。一质量为$m$、电荷量为$+q$的绝缘小球$A$从$M$点出发,以初速度$v_{0}$水平向右从$N$点进入右侧电场区域,并且从$O$点进入第一象限。已知$OP=2NP$,匀强电场场强大小$E= \dfrac{2mg}{q}$,匀强磁场磁感应强度大小$B= \dfrac{mg}{qv_{0}}$。小球$A$可视为质点,全过程小球$A$电荷量保持不变,不计空气阻力,重力加速度为$g$。求:
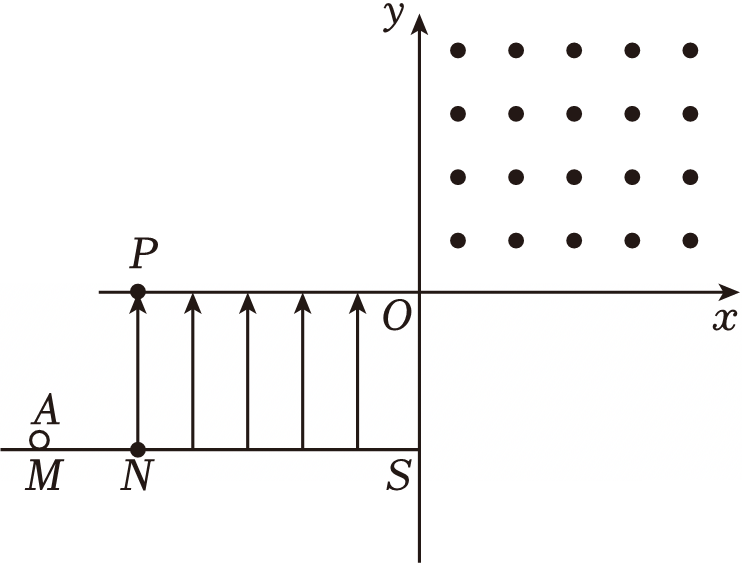
小球$A$到达$O$点时的速度;
$\\sqrt{2}v_{0}$;
"]]小球进入电场区域后在重力和电场力作用下做类平抛运动,设$OP=2\;\rm L$,$NP=L$到达$O$点时与$x$轴夹角为$\alpha$,则有
$2 L=v_{0}t$,$L=\dfrac{1}{2}at^{2}$
$qE-mg=ma$
$v_{y}=at$,$v_{1}=\sqrt{v_{0}^{2}+v_{y}^{2}}$
$\tan\alpha=\dfrac{v_{y}}{v_{0}}$
解得$v_{1}=\sqrt{2}v_{0}$
$\alpha=45^\circ$
小球$A$在第一次进入第一象限后轨迹最高点的纵坐标$y$。
$\\dfrac{(\\sqrt{5}-2)v_{0}^{2}}{g}$
"]]解法一:
小球从$O$点进入第一象限后在重力和洛伦兹力的作用下发生偏转,第一次到达最高点时其速度沿水平方向,假设最高点速度为$v_{2}$,最高点的纵坐标为$y$,由$O$到最高点只有重力做功,故$- mgy=\dfrac{1}{2}mv_{2}^{2}-\dfrac{1}{2}mv_{1}^{2}$
分解$v_{1}$,假设其水平分速度为$v_{1x}$,竖直分速度为$v_{1y}$,从$O$点到最高点所用时间为$t$,对小球列水平方向动量定理则有
$∑qv_{1}Bt=qBy=mv_{2}-mv_{1x}$
$v_{1x}=v_{0}$
代入数据解得$y=\dfrac{(\sqrt{5}-2)v_{0}^{2}}{g}$
解法二:
进入第一象限之后,将运动分解成为水平向左的速度为$v_{0}$的匀速直线运动和速度为$v_{2}$的顺时针方向的匀速圆周运动,到最高点时速度为$v_{2}-v_{0}$,如图所示
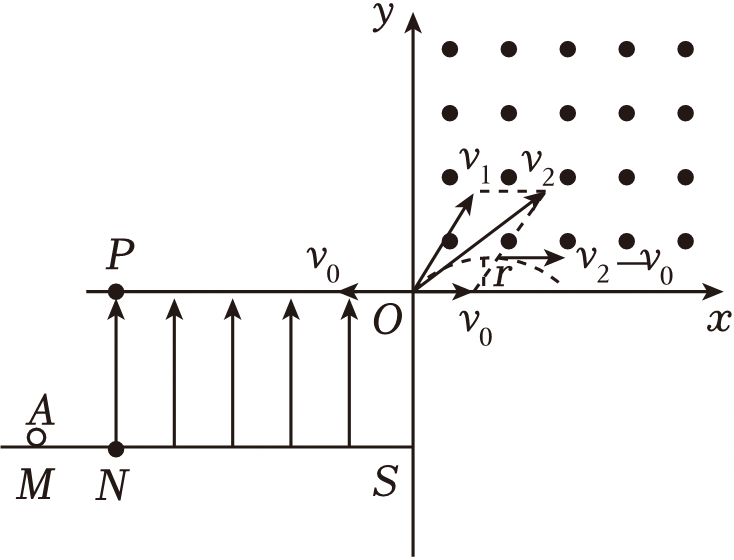
$- mgy=\dfrac{1}{2}m{(v_{2}-v_{0})}^{2}-\dfrac{1}{2}mv_{1}^{2}$
$v_{2}=\sqrt{5}v_{0}$
代入数据解得$y=\dfrac{(\sqrt{5}-2)v_{0}^{2}}{g}$
| 运动的合成与分解题目答案及解析(完整版)
