| 运动的合成与分解 题目答案及解析
稿件来源:高途
| 运动的合成与分解题目答案及解析如下,仅供参考!
必修2
第五章 曲线运动
5.1 曲线运动
运动的合成与分解
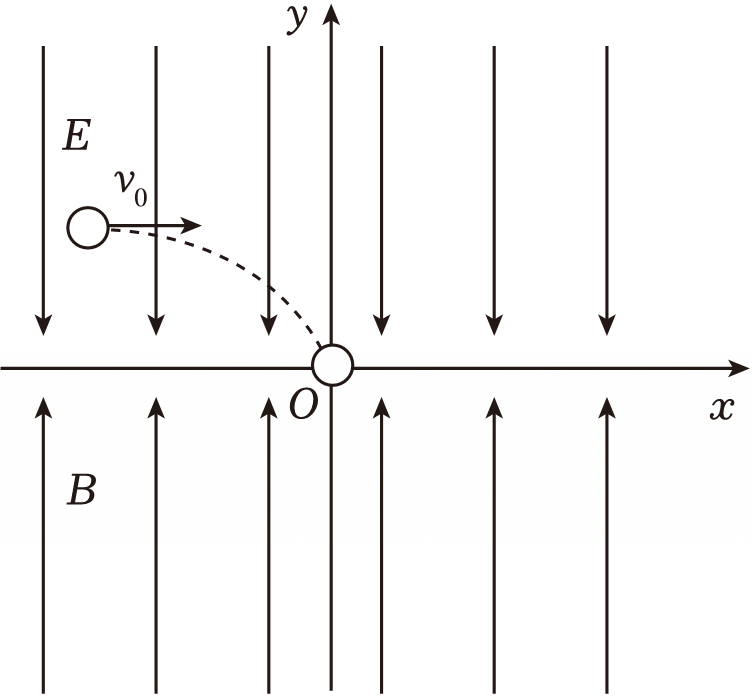
如图所示,在竖直平面直角坐标系中,$x$轴上方空间覆盖有方向竖直向下的匀强电场,电场强度大小未知;$x$轴下方空间覆盖有方向竖直向上的匀强磁场,磁感应强度大小为$B$。一质量为$3m$、电量为$2q$的带正电金属小球$M$,由第二象限中的某点沿$x$轴正方向以大小为$v_{0}$的速度水平抛出,经过时间$\dfrac{v_{0}}{g}$后,小球$M$以与$x$轴正方向成$53^\circ$角的速度到达坐标原点$O$,刚好与在$O$点静止释放的金属小球$N$弹性正碰;已知金属小球$N$质量为$m$,开始不带电,与小球$M$碰后,获得小球$M$一半电量:两球可以看成质点,忽略碰后两球间电荷的作用力和空气阻力,重力加速度大小为$g$,$\sin53^\circ=0.8$,求:
匀强电场的电场强度大小$E$;
$\\dfrac{mg}{2q}$;
"]]小球$M$被水平抛出后做类平抛运动,到达$O$点时的水平分速度为$v_{0}$,设其到达$O$点时的竖直分速度为$v_{y}$,已知小球$M$以与$x$轴正方向成$53^\circ$角的速度到达坐标原点$O$,则有:$\tan53{^\circ}=\dfrac{v_{y}}{v_{0}}$,解得:$v_{y}=\dfrac{4}{3}v_{0}$
小球$M$在电场中运动的加速度大小为:$a=\dfrac{v_{y}}{t}=\dfrac{4}{3}g$
根据牛顿第二定律得:$2qE+3mg=3ma$
解得:$E=\dfrac{mg}{2q}$
两球碰后瞬间的速度大小$v_{M}$、$v_{N}$;
$\\dfrac{5}{6}v_{0}$、$\\dfrac{5}{2}v_{0}$;
"]]小球$M$到达$O$点时的速度大小为:$v= \dfrac{v_{0}}{\cos53{^\circ}}=\dfrac{5v_{0}}{3}$
两球发生弹性碰撞,以小球$M$到达$O$点时的速度方向为正方向,根据动量守恒定律与机械能守恒定律得:
$3mv=3mv_{M}+mv_{N}\dfrac{1}{2} \times 3mv^{2}=\dfrac{1}{2} \times 3mv_{M}^{2}+\dfrac{1}{2}mv_{N}^{2}$
解得:$v_{M}=\dfrac{5}{6}v_{0}$,$v_{N}=\dfrac{5}{2}v_{0}$
从两球碰后瞬间开始计时,求在$t= \dfrac{3k\pi m}{qB}(k=1,2,3 \cdots )$时刻,两球距离的表达式。
$\\dfrac{4k\\pi mv_{0}}{qB}(k=1,2,3 \\cdots)$
"]]碰后小球$M$、$N$带电量均为$q$,两小球进入磁场时沿$+x$方向与$-y$方向的分速度分别为:
$v_{Mx}=v_{M}\cos53^\circ= \dfrac{1}{2}v_{0}$,$v_{My}=v_{M}\sin53^\circ= \dfrac{2}{3}v_{0}$,$v_{Nx}=v_{N}\cos53^\circ= \dfrac{3}{2}v_{0}$,$v_{Ny}=v_{N}\sin53^\circ=2v_{0}$
两小球均沿$-y$方向做加速度等于$g$的匀加速运动,均在水平面内做匀速圆周运动,运动轨迹为不等距的螺旋线。
对于匀速圆周运动,由洛伦兹力提供向心力得:
$qv_{Mx}B=3m\dfrac{v_{Mx}^{2}}{r_{M}}$;$qv_{Nx}B=m\dfrac{v_{Nx}^{2}}{r_{N}}$
解得小球$M$、$N$的圆周运动半径为$r_{M}=r_{N}= \dfrac{3mv_{0}}{2qB}$
小球$M$圆周运动的周期为:$T_{M}=\dfrac{2\pi r_{M}}{v_{Mx}}=\dfrac{6\pi m}{qB}$
小球$N$圆周运动的周期为:$T_{N}=\dfrac{2\pi r_{N}}{v_{Nx}}=\dfrac{2\pi m}{qB}$
从两球碰后瞬间开始计时,在$t=\dfrac{3k\pi m}{qB}(k=1,2,3 \cdots )$时刻,两球总是在同一竖直线上。
根据碰后两球在竖直方向上的分运动,可得两球的距离的表达式为:
$d=y_{N}-y_{M}=v_{Ny}t+ \dfrac{1}{2}gt^{2}-\left(v_{My}t+ \dfrac{1}{2}gt^{2}\right)=(v_{Ny}-v_{My})t= \dfrac{4k\pi mv_{0}}{qB}(k=1,2,3 \cdots)$
| 运动的合成与分解题目答案及解析(完整版)
