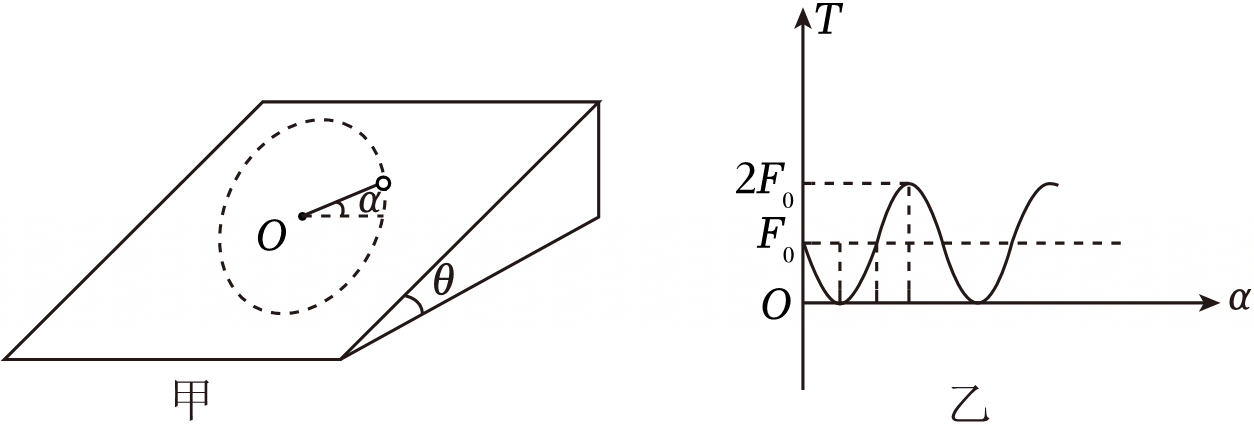
如图甲所示，倾角为$\theta$的光滑斜面固定在水平地面上，细线一端与可看成质点的质量为$m$的小球相连，另一端穿入小孔$O$与力传感器（位于斜面体内部）连接，传感器可实时记录细线拉力大小及扫过的角度。初始时，细线水平，小球位于小孔$O$的右侧，现敲击小球，使小球获得一平行于斜面向上的初速度$v_{0}$，测得细线拉力$T$的大小随细线扫过角度$\alpha$的变化图像如图乙所示，图中$F_{0}$已知，小球到$O$点距离为$l$，重力加速度为$g$，则下列说法正确的是$(\qquad)$

小球位于初始位置时的加速度大小为$\\dfrac{v_{0}^{2}}{l}$

小球通过最高点时速度大小为$\\sqrt{gl}$

小球通过最高点时速度大小为$v_{0}\\sqrt{\\dfrac{mg\\sin\\theta}{F_{0}}}$

小球通过最低点时速度大小为$v_{0}\\sqrt{\\dfrac{F_{0}-mg\\sin\\theta}{F_{0}}}$

$\rm A$．小球位于初始位置时的向心加速度为$a_{1}=\dfrac{v_{0}^{2}}{l}$，沿斜面向下的加速度为$a_{2}=g\sin\theta$，根据加速度的合成知识可知，小球位于初始位置时的加速度大于$\dfrac{v_{0}^{2}}{l}$，故$\rm A$错误；

$\rm B$．由图乙可知，小球通过最高点时细线的拉力为零，在斜面上重力和支持力的合力提供向心力，则有$mg\sin\theta=m\dfrac{v_{1}^{2}}{l}$，解得$v_{1}=\sqrt{gl\sin\theta}$，故$\rm B$错误；

$\rm C$．小球在初始位置时，有$F_{0}=m\dfrac{v_{0}^{2}}{l}$，则小球通过最高点时速度为$v_{1}=\sqrt{gl\sin\theta}=\sqrt{\dfrac{mg\sin\theta}{F_{0}}}v_{0}$，故$\rm C$正确；

$\rm D$．小球通过最低点时，有$2F_{0}-mg\sin\theta=m\dfrac{v_{2}^{2}}{l}$，解得小球通过最低点的速度为$v_{2}=\sqrt{\dfrac{2F_{0}-mg\sin\theta}{F_{0}}}v_{0}$，故$\rm D$错误。

故选：$\rm C$。