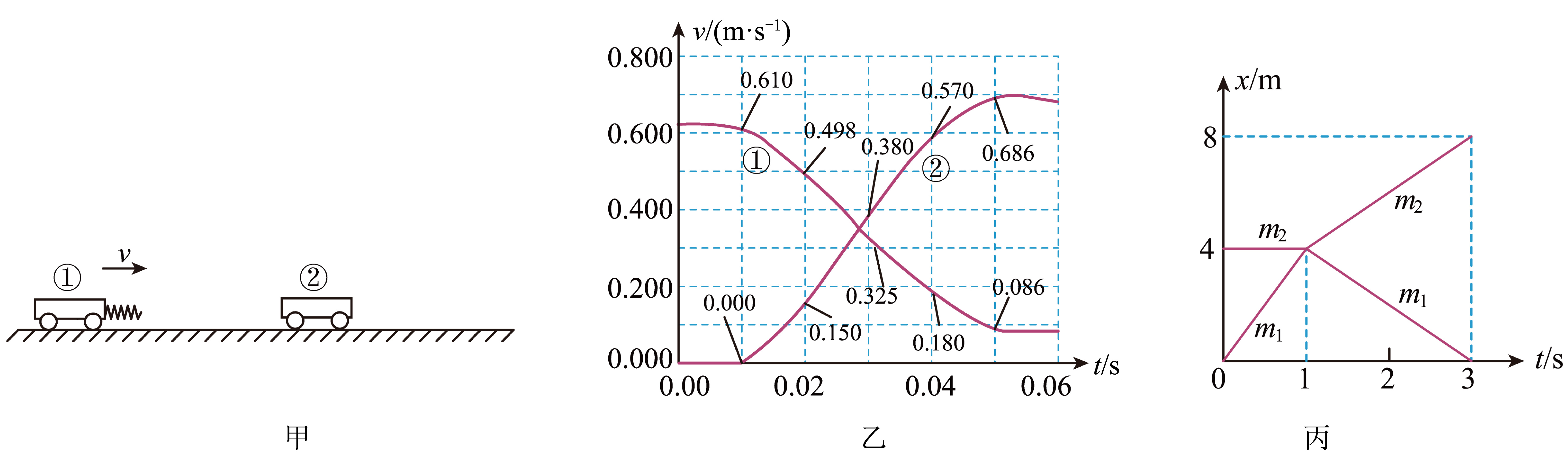
碰撞过程中，两车间的相互作用力$(\quad\ \ \ \ )$；

保持不变

持续增大

先增大后减小

先减小后增大

由$v − t$图像可知加速度先增大后减小，根据牛顿第二定律可知两车间的相互作用力先增大后减小；

故选：$\rm C$；

碰撞过程中弹簧弹性势能的最大值最接近$(\quad\ \ \ \ )$；

$0.007\\;\\rm J$

$0.018\\;\\rm J$

$0.025\\;\\rm J$

$0.050\\;\\rm J$

由图$2$可知两车共速的速度约为$0.350\;\rm m/s$，小车$1$初始速度为$0.610\;\rm m/s$，根据能量守恒定律有$\Delta E_{\rm p}=\dfrac{1}{2}m_{1}v_{0}^{2}- \dfrac{1}{2}(m_{1}+m_{2})v^{2}$

代入数据解得$\Delta E_{\rm p}=0.025\;\rm J$；

故选：$\rm C$；

（计算）该同学对实验结果进行误差分析，发现碰撞过程中两车动量之和实际在不断减少，他认为是轨道对车的摩擦力引起的。求碰撞过程中小车$1$受到的平均摩擦力大小；

$0.3\\;\\rm N$

碰撞过程中两车总动量变化$\Delta p_{总}=(m_{1}v_{1}'+m_{2}v_{2}')− (m_{1}v_{1}+m_{2}v_{2})$

解得$\Delta p_{总}=-0.02\;\rm kg ⋅ m/s$

其中碰撞时间$\Delta t=0.04\;\rm s$

碰撞过程中摩擦力对两车总冲量$I_{总}=I_{f1}+I_{f2}=f_{1}\Delta t+f_{2}\Delta t=\Delta p_{总}$

摩擦力$f=\mu N=\mu mg$

所以$f_{1}:f_{2}=m_{1}:m_{2}=3:2$

代入可得$f_{1}=-0.3\;\rm N$

故碰撞过程中小车$1$受到的平均摩擦力大小为$0.3\;\rm N$；

若质量为$m_{1}$和$m_{2}$的两个小车在一水平轨道上发生碰撞，其位移$x$与时间$t$的关系图像如图丙所示，碰撞时间很短，可忽略不计。

①（计算）$m_{1}$与$m_{2}$的比值；

②（论证）两个物体的碰撞是弹性碰撞还是非弹性碰撞？

①$m_{1}$与$m_{2}$的比值为$\\dfrac{1}{3}$；②两小车的碰撞是弹性碰撞

①对两小车所构成的系统，碰撞后均做匀速直线运动，沿碰撞方向外力为零，系统动量守恒有$m_{1}v_{10}+m_{2}v_{20}=m_{1}v_{1}+m_{2}v_{2}$

其中$v=\dfrac{\Delta x}{\Delta t}$

由图$v_{10}=4\;\rm m/s$，$v_{20}=0$，$v_{1}=-2\;\rm m/s$，$v_{2}=2\;\rm m/s$

可得$\dfrac{m_{1}}{m_{2}}=\dfrac{1}{3}$

②碰撞前后动量和动能都不变的碰撞称为弹性碰撞。对两小车所构成的系统，碰撞后均做匀速直线运动，沿碰撞方向外力为零，碰撞前后系统动量变化$\Delta p=0$

碰撞前后系统动能变化$\Delta E_{\rm{k}}=\dfrac{1}{2}m_{1}v_{10}^{2}+\dfrac{1}{2}m_{2}v_{20}^{2}-\dfrac{1}{2}m_{1}v_{1}^{2}-\dfrac{1}{2}m_{2}v_{2}^{2}$

代入数据解得$\Delta E_{\rm k}=0$

故两小车的碰撞是弹性碰撞。