高中 | 示波管 题目答案及解析
稿件来源:高途
高中 | 示波管题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
示波管
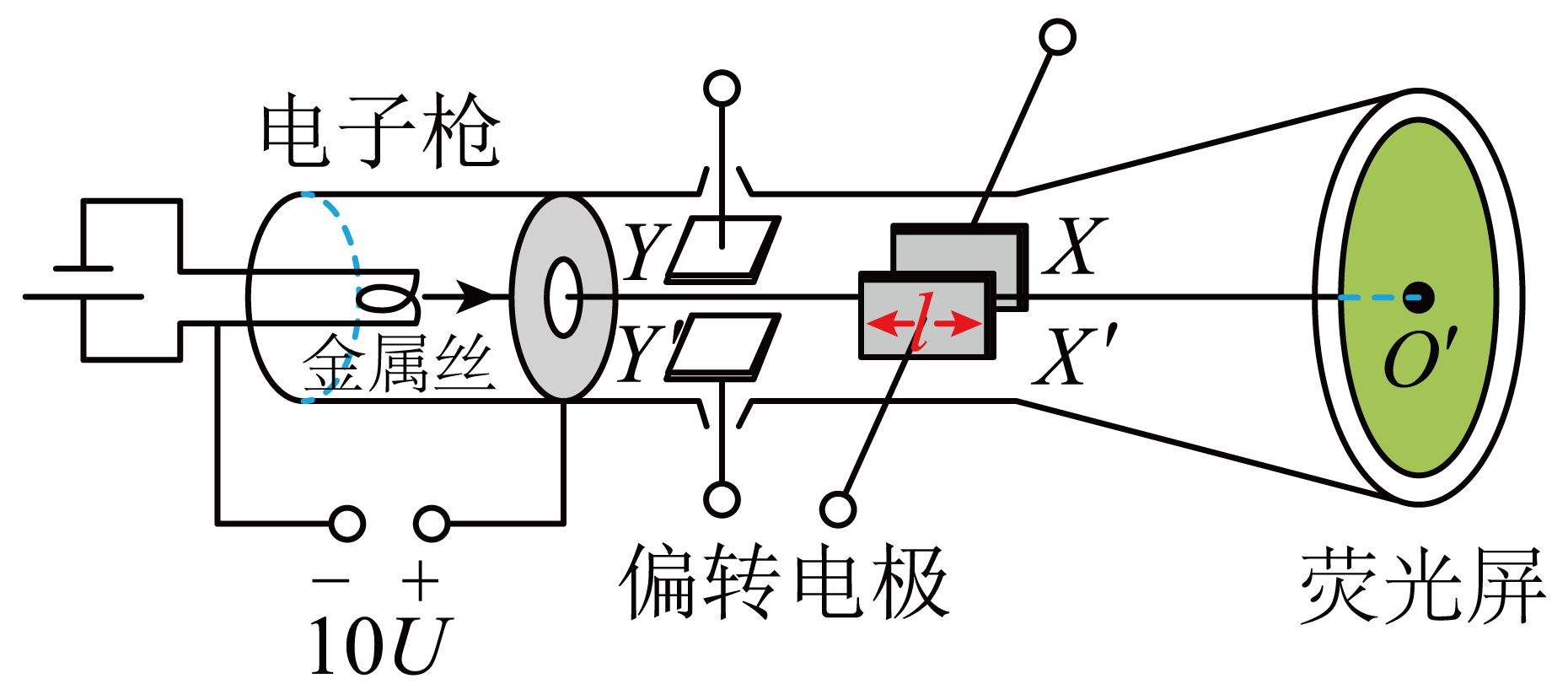
如图所示,示波管由电子枪、竖直方向偏转电极$'$、水平方向偏转电极$XX'$和荧光屏组成。电极$XX'$的长度为$l$、间距为$d$、极板间电压为$U$,电极$XX'$的右边缘距荧光屏的水平距离为$s$。$'$极板间电压为零,电子枪加速电压为$10U$。电子刚离开金属丝的速度为零,从电子枪射出后沿$OO'$方向进入偏转电极。已知电子电荷量为$e$,质量为$m$,则电子$(\qquad)$
以$v_{0}=\\sqrt{\\dfrac{20eU}{m}}$的速度水平进入偏转电极$XX'$
","离开偏转电极$XX'$时的速度为$v=\\sqrt{\\dfrac{22eU}{m}}$
","打到荧光屏上的位置距$O'$点的水平距离为$x=d+\\dfrac{sl}{20d}$
","从进入偏转电极$XX'$开始到打到荧光屏所经历的时间为$t=(l+s)\\sqrt{\\dfrac{m}{20eU}}$
"]$\rm A$.根据动能定理$10Ue=\dfrac{1}{2}mv_{0}^{2}$
解得电子水平进入偏转电极$XX'$的速度$v_{0}=\sqrt{\dfrac{20eU}{m}}$,选项$\rm A$正确;
$\rm B$.电子在偏转电极$XX'$时$l=v_{0}t$,$a=\dfrac{Ue}{dm}$
离开偏转电极时$v_{y}=at=\dfrac{Uel}{dmv_{0}}=\dfrac{l}{d}\sqrt{\dfrac{eU}{20m}}$
合速度为$v=\sqrt{v_{0}^{2}+v_{y}^{2}}=\sqrt{\dfrac{eU}{20d^{2}m}(400d^{2}+l^{2})}$,选项$\rm B$错误;
$\rm C$.出离偏转电极时速度的偏转角$\tan\theta=\dfrac{v_{y}}{v_{0}}=\dfrac{l}{20d}$
打到荧光屏上的位置距$O'$点的水平距离为$x=\left(s+\dfrac{l}{2}\right)\tan\theta=\left(s+\dfrac{l}{2}\right)\dfrac{l}{20d}$,选项$\rm C$错误;
$\rm D$.从进入偏转电极$XX'$开始到打到荧光屏水平方向一直做匀速运动,则所经历的时间为$t=\dfrac{l+s}{v_{0}}=(l+s)\sqrt{\dfrac{m}{20eU}}$,选项$\rm D$正确。
故选:$\rm AD$。
高中 | 示波管题目答案及解析(完整版)
