高中 | 示波管 题目答案及解析
稿件来源:高途
高中 | 示波管题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
示波管
有一种电子仪器叫作示波器,可以用来观察电信号随时间变化的情况。示波器的核心部件是示波管,图甲是它的原理图。它由电子枪、偏转电极和荧光屏组成,管内抽成真空。电子枪的作用是产生高速飞行的一束电子。如果在偏转电极$XX'$之间和偏转电极$YY'$之间都没有加电压,电子束从电子枪射出后沿直线运动,打在荧光屏中心,在那里产生一个亮斑。如果示波管的$YY'$偏转电极上加的是如图丙所示的待测的信号电压,$XX'$偏转电极接入仪器自身产生的如图丁所示的锯齿形扫描电压,电子质量为$m$,带电量为$−e$,初速度为$0$,加速电压为$U_{1}$,$YY'$之间的距离为$d_{1}$,左右方向长度为$l_{1}$,$XX'$之间的距离为$d_{2}$,左右方向的长度为$l_{2}$,$X'$右侧到荧光屏的距离为$l_{3}$。电子在示波管中的运动时间远小于$T$,不计偏转电极$XX'$与$YY'$之间的水平距离,求
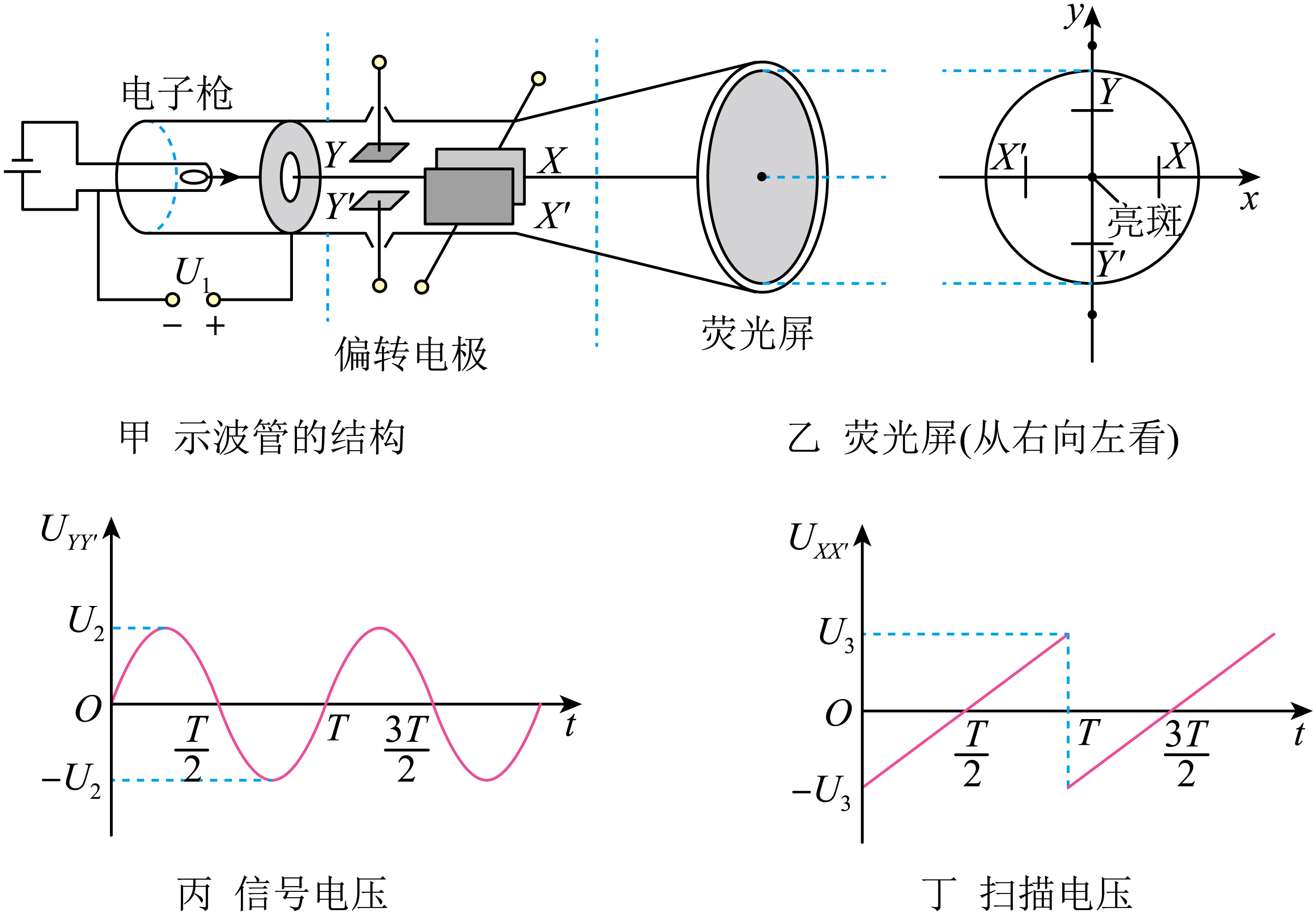
$0\sim T$内任意时刻$t$荧光屏上的亮斑的$x$坐标;
$x=\\dfrac{\\left( l_{2}+2l_{3} \\right)l_{2}U_{3}(2t-T)}{4U_{1}d_{2}T}$;
"]]设电子在加速电场中被加速后的速度为$v_{0}$,则有$eU_{1}=\dfrac{1}{2}mv_{0}^{2}$
故偏转电极$XX'$之间的电压为$U_{{XX}'}=\dfrac{2t}{T}U_{3}-U_{3}$
电子在偏转电极$XX'$之间运动加速度$a_{x}=\dfrac{eU_{{X}{X}'}}{md_{2}}$
运动时间$t_{x}=\dfrac{l_{2}}{v_{0}}$
故$v_{x}=a_{x}t_{x}$,$\tan\alpha=\dfrac{v_{x}}{v_{0}}$
故$x=\dfrac{1}{2}a_{x}t_{x}^{2}+l_{3}\tan\alpha$(或$x=\left( \dfrac{l_{2}}{2}+l_{3} \right)\tan\alpha$)
解得$x=\dfrac{\left( l_{2}+2l_{3} \right)l_{2}U_{3}(2t-T)}{4U_{1}d_{2}T}$;
$0\sim T$内任意时刻$t$荧光屏上的亮斑的$y$坐标;
$y=\\dfrac{\\left( l_{1}+2l_{2}+ 2l_{3} \\right)l_{1}U_{2}\\sin\\left( \\dfrac{2\\pi}{T}t \\right)}{4U_{1}d_{1}}$
"]]偏转电极$YY'$之间电压$U_{{Y}{Y}'}=U_{2}\sin\left( \dfrac{2\pi}{T}t \right)$;
电子在偏转电极$YY'$之间运动加速度$a_{y}=\dfrac{eU_{{Y}{Y}'}}{md_{1}}$
运动时间$t_{y}=\dfrac{l_{1}}{v_{0}}$
故$v_{y}=a_{y}t_{y}$,$\tan\theta=\dfrac{v_{y}}{v_{0}}$
故$y=\dfrac{1}{2}a_{y}t_{y}^{2}+\left( l_{2}+l_{3} \right)\tan\theta$(或$y=\left( \dfrac{l_{1}}{2}+l_{2}+l_{3} \right)\tan\theta$)
解得$y=\dfrac{\left( l_{1}+2l_{2}+2l_{3} \right)l_{1}U_{2}\sin\left( \dfrac{2\pi}{T}t \right)}{4U_{1}d_{1}}$;
由于$T$比视觉暂留时间(约为$0.1\;\rm s$)小得多,所以观察者在荧光屏上看到的是稳定的亮线,请在坐标纸上画出$x$、$y$坐标轴,先求出$x$、$y$坐标的最大值,再画出亮线的图像。
见解析
"]]由$x=\dfrac{\left( l_{2}+2l_{3} \right)l_{2}U_{3}(2t- T)}{4U_{1}d_{2}T}$可知,$0\sim T$内当$t=T$时$x$坐标达到最大值$x_{\rm{m}}=\dfrac{\left( l_{2}+2l_{3} \right)l_{2}U_{3}}{4U_{1}d_{2}}$
由$y=\dfrac{\left( l_{1}+2l_{2}+2l_{3} \right)l_{1}U_{2}\sin\left( \dfrac{2\pi}{T}t \right)}{4U_{1}d_{1}}$可知,$0\sim T$内当$t=\dfrac{T}{4}$时$y$坐标达到最大值$y_{\rm{m}}=\dfrac{\left( l_{1}+2l_{2}+2l_{3} \right)l_{1}U_{2}}{4U_{1}d_{1}}$
故图像为
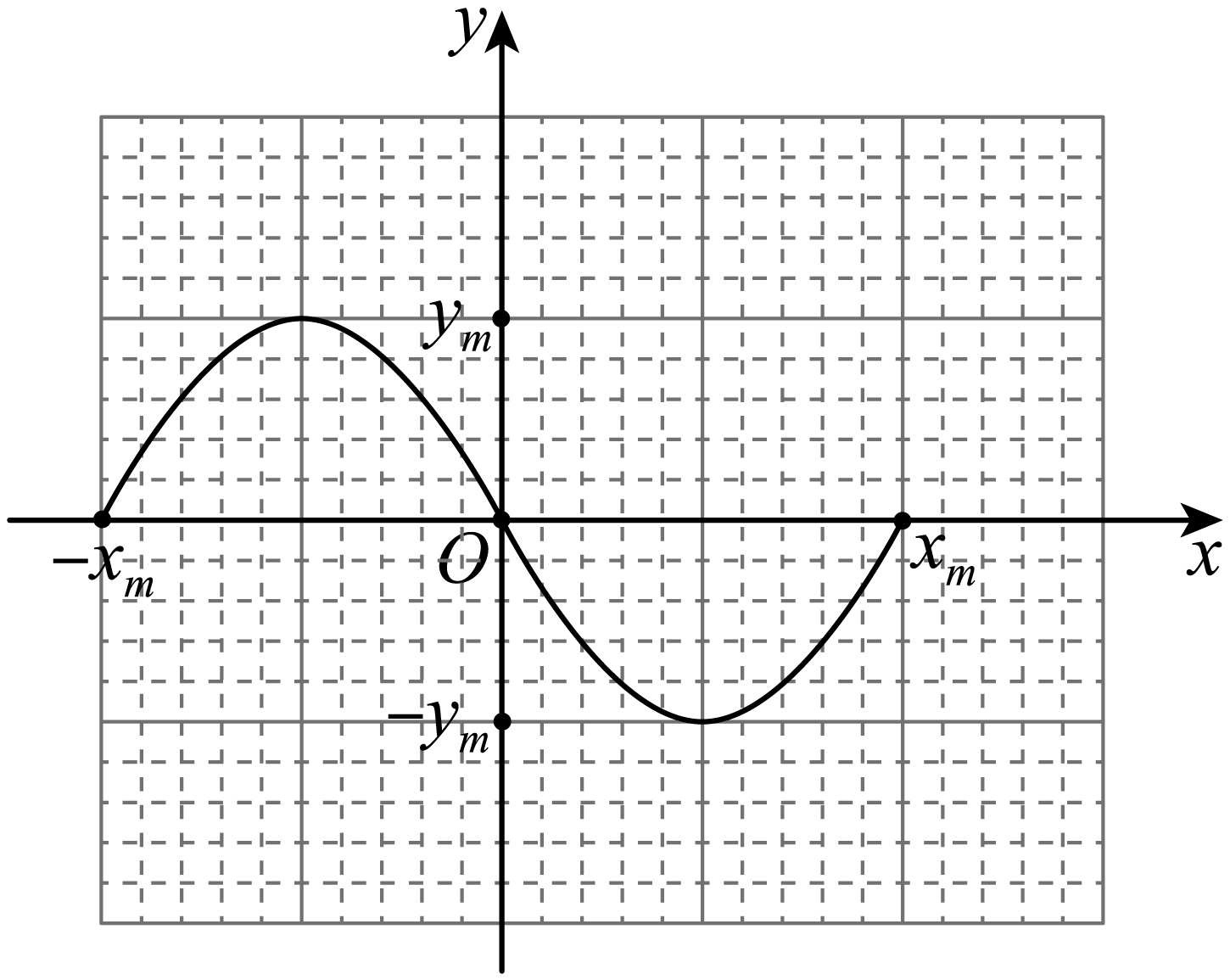
高中 | 示波管题目答案及解析(完整版)
