高中 | 示波管 题目答案及解析
稿件来源:高途
高中 | 示波管题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
示波管
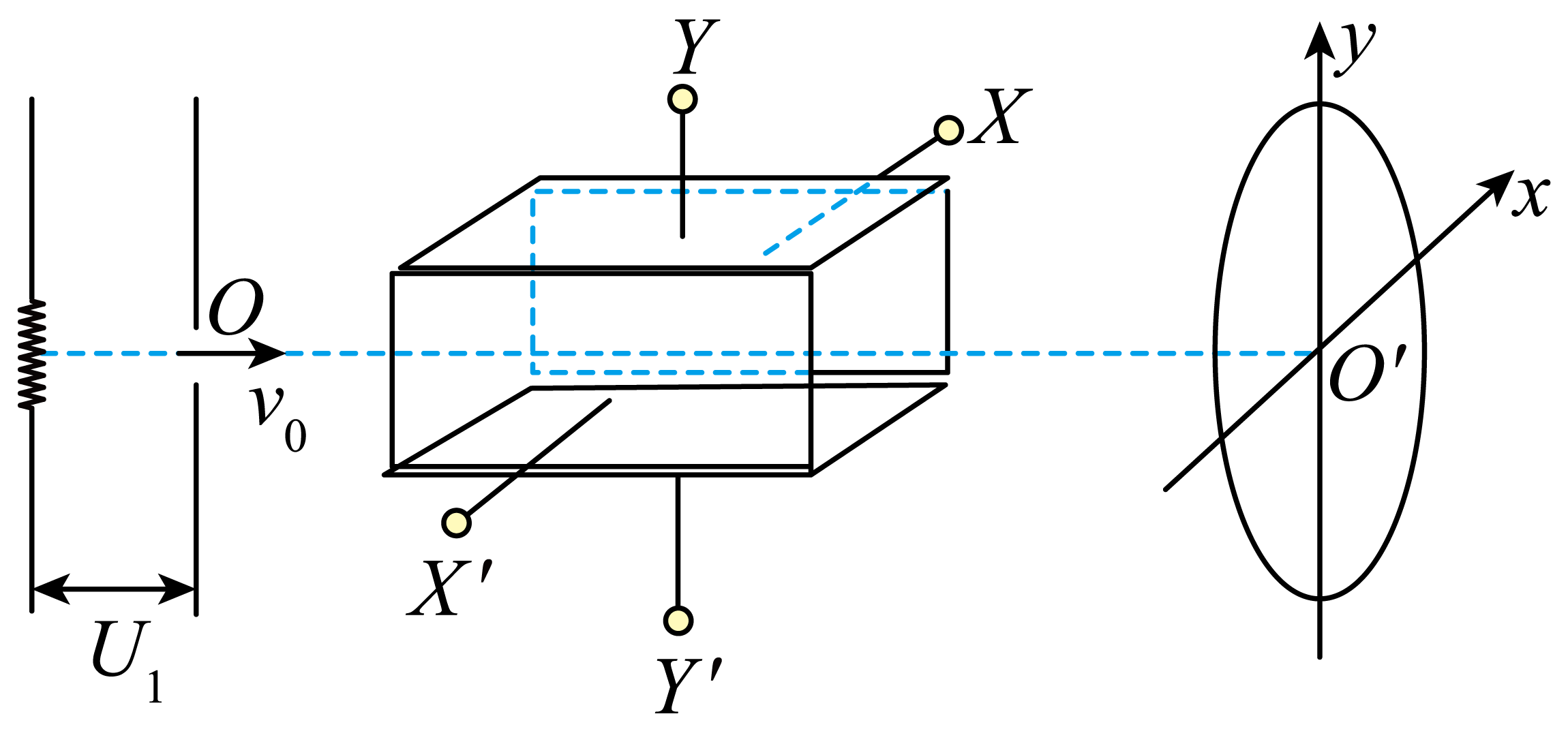
示波器的核心部件是示波管,它由电子枪、偏转电极、荧光屏组成。某示波管示意图如图所示,炽热的金属丝可以连续发射出电子(初速度视为零),电子经加速电场加速后沿中央轴线$OO'$垂直进入偏转电场,加速电压$U_{1}=180\;\rm V$,偏转电场由两对偏转电极$XX'$、$YY'$组成,位置如图所示,均以$OO'$为中央轴线,极板长度均为$L_{1}=8\;\rm cm$,极板$X$与$X'$的间距、极板$Y$与$Y'$的间距均为$d=4\;\rm cm$。电子穿出偏转电场后做匀速直线运动,直到打在荧光屏上,极板右边缘到荧光屏距离$L_{2}=20\;\rm cm$,$O'$为荧光屏正中心,并在荧光屏上建立$xO'y$坐标系。已知电子质量$m=9.0 \times 10^{-31}\;\rm kg$、电荷量$e=1.6 \times 10^{-19}\;\rm C$,不计电子受到的重力和电子之间的相互作用力,极板$X$与$X'$,极板$Y$与$Y'$极板间的匀强电场互不影响,忽略电场边缘效应。
求电子经加速电场加速后的速度$v_{0}$;
$8 \\times 10^{6}\\;\\rm m/s$;
"]]电子在加速电场中运动,根据动能定理有$eU_{1}=\dfrac{1}{2}mv_{0}^{2}$
代入数据解得$v_{0}=8 \times 10^{6}\;\rm m/s$;
若$XX'$、$YY'$间分别输入$U_{XX'}=30\;\rm V$,$U_{YY'}=60\;\rm V$的恒定电压,求电子刚离开偏转电场时,在$XX'$和$YY'$方向上的偏转量$x_{1}$和$y_{1}$;
见解析
"]]当$U_{XX'}=30\;\rm V$时,水平方向$L_{1}=v_{0}t$
代入数据解得$t=\dfrac{8 \times 10^{- 2}}{8 \times 10^{6}}\;\rm{s}=1 \times 10^{- 8}\;\rm {s}$
沿$XX'$方向,根据牛顿第二定律有$a_{x}=\dfrac{eU_{XX'}}{md}=\dfrac{1.6 \times 10^{- 19} \times 30}{9.0 \times 10^{- 31} \times 0.04}\;\rm{m}/{s}^{2}=\dfrac{4}{3} \times 10^{14}\;\rm{m}/{s}^{2}$
根据位移时间公式可得$x_{1}=\dfrac{1}{2}a_{x}t^{2}=\dfrac{2}{3}\;\rm{cm}$
当$U_{YY'}=60\;\rm V$时,水平方向$L_{1}=v_{0}t$
沿$YY'$方向,根据牛顿第二定律有$a_{y}=\dfrac{eU_{YY'}}{md}\dfrac{1.6 \times 10^{- 19} \times 60}{9.0 \times 10^{- 31} \times 0.04}\;\rm{m}/{s}^{2}=\dfrac{8}{3} \times 10^{14}\;\rm{m}/{s}^{2}$
根据位移时间公式可得$y_{1}=\dfrac{1}{2}a_{y}t^{2}=\dfrac{4}{3}\;\rm{cm}$;
若$XX'$、$YY'$间分别输入$U_{XX'}=30\sin100\pi t\:\rm(V)$,$U_{YY'}=60\sin100\pi t\:\rm(V)$的交变电压,其中$t$的单位为$s$。求电子打在荧光屏上的亮线长度。
$8\\sqrt{5}\\;\\rm{cm}$。
"]]当$U_{XX'}=30\sin100\pi t\:\rm(V)$时,根据速度时间公式有$v_{x}=a_{x}t$
根据几何关系有$\tan\theta_{x}=\dfrac{v_{x}}{v_{0}}$
沿$XX'$方向,电子打在荧光屏上离$O'$最大距离$x_{2}=\tan\theta_{x}(L+\dfrac{L_{1}}{2})$
解得$x_{2}=4\;\rm cm$
当$U_{YY'}=60\sin100\pi t\:\rm(V)$时,根据速度时间公式有$v_{y}=a_{y}t$
根据几何关系可得$\tan\theta_{y}=\dfrac{v_{y}}{v_{0}}$
则有$y_{2}=\tan\theta_{y}\left(L+\dfrac{l}{2}\right)$
解得$y_{2}=8\;\rm cm$
荧光屏上出现的是以$A$($4\;\rm cm$,$8\;\rm cm$),$B$($− 4\;\rm cm$,$− 8\;\rm cm$)两点为端点的一条线段
电子打在荧光屏上的亮线长度为$s=\sqrt{\left\lbrack 4-(-4) \right\rbrack^{2}+\left\lbrack 8-(-8) \right\rbrack^{2}}\;\rm{cm}=8\sqrt{5}\;\rm {cm}$。
高中 | 示波管题目答案及解析(完整版)
