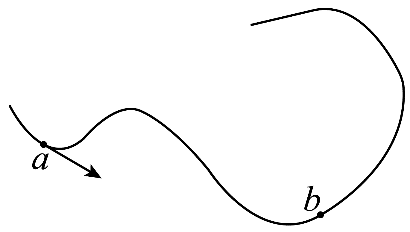
与$a$点运动方向相同的点有                 个（选涂： $\rm A$．$1$    $\rm B$．$2$    $\rm C$．$3$）

曲线运动中某点的速度方向是曲线在该点的切线方向，在上面的曲线运动中，和$a$点速度相同的方向应该有$2$个；

故选：$\rm B$；

$a$、$b$两点的角速度的关系：$\omega_{a}$                 $\omega_{b}$（选涂：$\rm A$．大于    $\rm B$．等于    $\rm C$．小于）

$a$点处的曲率半径小于$b$点处的曲率半径，根据$v=R\omega$可知$\omega a\gt \omega b$

故选：$\rm A$；

《天工开物》中记载了古人借助水力使用高转筒车往稻田里引水的场景。引水过程简化如下：两个半径均为$R$的水轮，以角速度$\omega$匀速转动。水筒在筒车上均匀排布，单位长度上有$n$个，与水轮间无相对滑动。每个水筒离开水面时装有质量为$m$的水，其中的$60\%$被输送到高出水面$H$处灌入稻田。当地的重力加速度为$g$，则筒车对灌入稻田的水做功的功率为$(\qquad)$

$\\dfrac{2nmg\\omega^{2}RH}{5}$

$\\dfrac{3nmg\\omega RH}{5}$

$\\dfrac{3nmg\\omega^{2}RH}{5}$

$nmg\\omega RH$

每个水筒中水的重力为$G=mg$，水筒的线速度为$v=\omega R$，取足够长的一段时间$t$内，装水的水筒个数为$N=nvt=n\omega Rt$，筒车对灌入稻田的水做功的功率为$P=\dfrac{W}{t}=\dfrac{60\% NGH}{t}= \dfrac{3nmg\omega RH}{5}$ ；

故选：$\rm B$；

水车是我国劳动人民利用水能的一项重要发明。下图为某水车模型，从槽口水平流出的水初速度大小为$v_{0}$，垂直落在与水平面成$30^\circ$角的水轮叶面上，落点到轮轴间的距离为$R$。在水流不断冲击下，设轮叶受冲击点的线速度大小接近冲击前瞬间水流速度大小，忽略空气阻力不计，有关水车及从槽口流出的水，水流在空中运动时间大小为                 ；水车最大线速度接近                 。

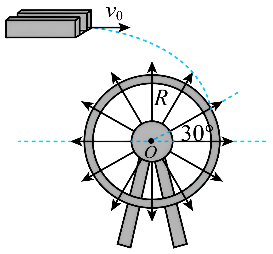
垂直落在与水平面成$30^\circ$角的水轮叶面上，可知$\tan 30^\circ= \dfrac{v_{0}}{gt}$。解得$t= \dfrac{\sqrt{3}v_{0}}{g}$。落到水轮叶面上时水的速度$v=\dfrac{v_{0}}{\sin 30^\circ}= 2v_{0}$。可知水车最大线速度接近$2v_{0}$。