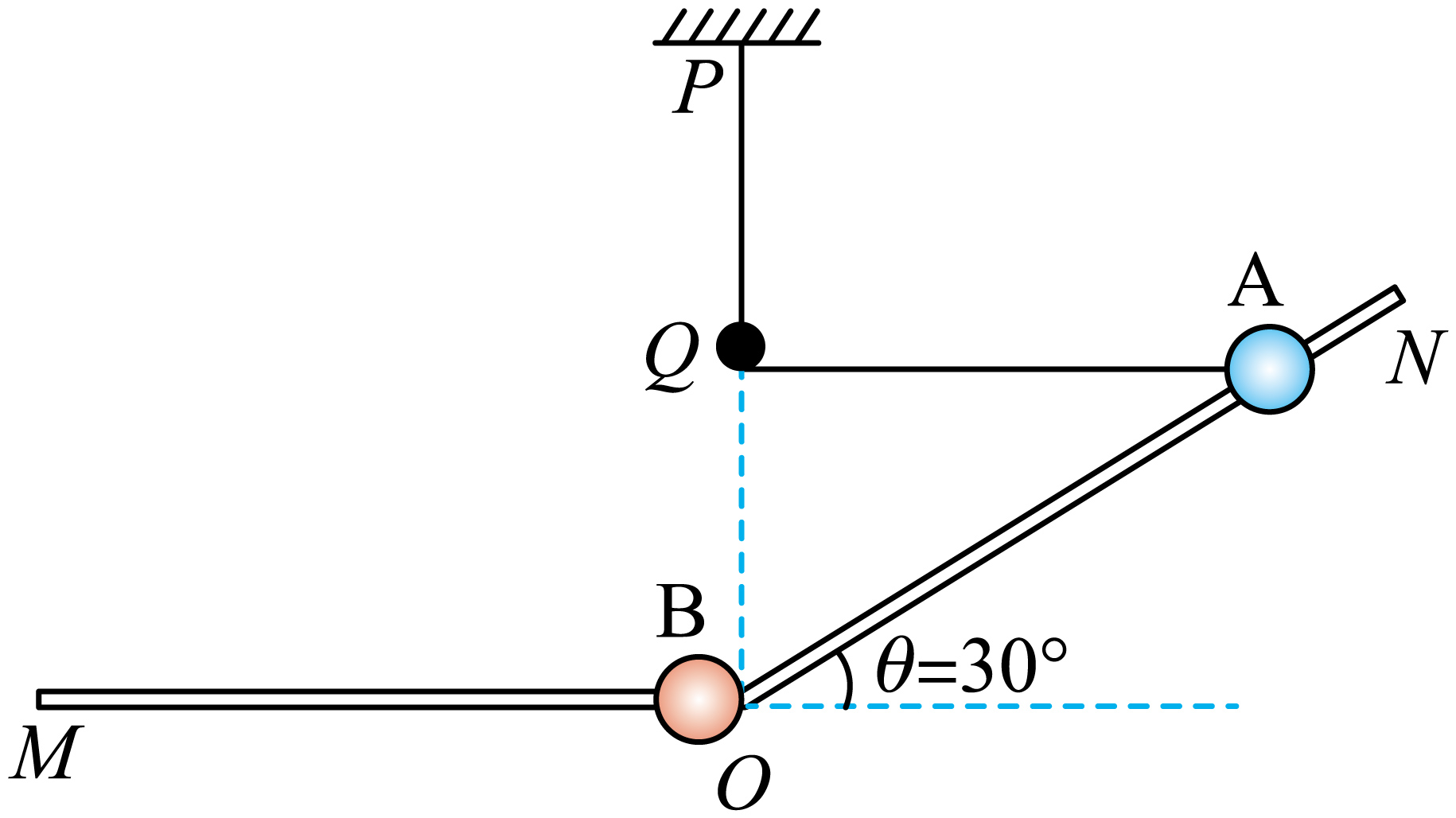
求小球$A$下滑过程中滑动摩擦力的大小；

$f=\\dfrac{1}{2}mg$

如图所示

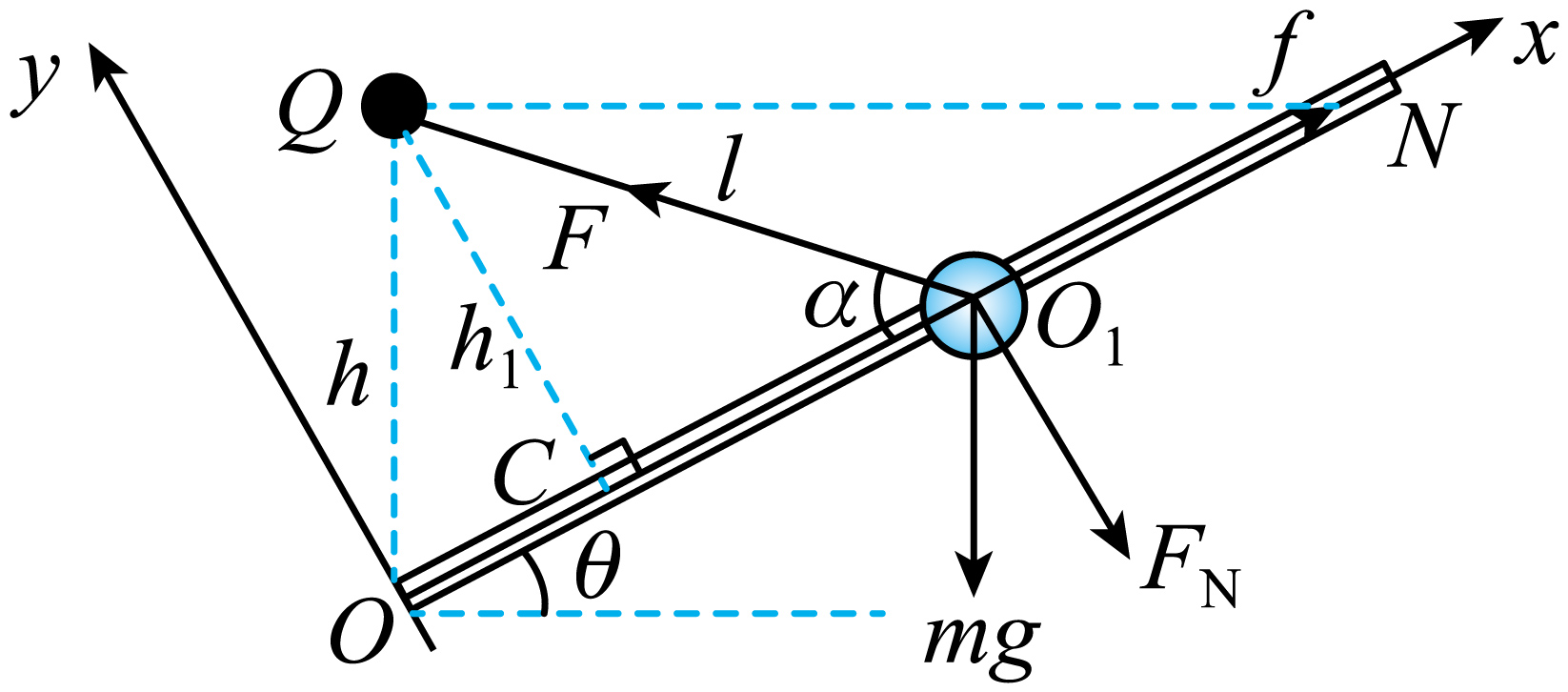
以$O$点为坐标原点，沿倾斜直杆$ON$向上为$x$轴正方向建立坐标系。任意选取小球$A$下滑过程中的某一位置$O_{1}$，设此时弹力绳的伸长量为$l$，小球$A$受到的滑动摩擦力为$f$，小球$A$对倾斜直杆的压力为$F_{N}$，小球$A$所受弹力绳的拉力为$F$，弹力绳与倾斜直杆的夹角为$\alpha$，孔钉$Q$到倾斜直杆的距离为$h_{1}$。设$h=\dfrac{2mg}{k}$

对小球$A$进行受力分析，可知$f=\mu F_{N}$，$F_{N}=F\sin \alpha − mg\cos \theta$，$F=kl$

由几何关系可得$h_{1}=l\sin \alpha=h\cos \theta$

联立解得$f=\dfrac{1}{2}mg$

若从碰撞后开始计时，小球$A$第一次上滑过程中离$O$点的距离$x$与时间$t$关系为$x=A_{0}\sin\left( \sqrt{\dfrac{k}{m}}t \right)$（$A_{0}$为常数），求小球$A$第一次速度为零时，小球$B$与$O$点的距离。

$s=\\left( \\dfrac{\\sqrt{2}}{2}\\pi- \\dfrac{\\sqrt{3}}{24}\\pi^{2} \\right)\\dfrac{mg}{k}$

设小球$A$下滑到斜杆底端$O$点时的速度为$v_{A}$，小球由静止释放运动到$O$点的过程中，由动能定理可得$- f \cdot 2h+mgh+\left\lbrack \dfrac{1}{2}k\left( \sqrt{3}h \right)^{2}-\dfrac{1}{2}kh^{2} \right\rbrack=\dfrac{1}{2}mv_{\text{A}}^{\text{2}}$

可得$\dfrac{1}{2}k\left( \sqrt{3}h \right)^{2}-\dfrac{1}{2}kh^{2}=\dfrac{1}{2}mv_{\text{A}}^{\text{2}}$

由小球$A$、$B$发生弹性碰撞后瞬间的速度分别为${v_{A}}'$、${v_{B}}'$，由动量守恒定律和能量守恒定律有$mv_{A}=m{v_{A}}'+3m{v_{B}}'$，$\dfrac{1}{2}mv_{\text{A}}^{\text{2}}=\dfrac{1}{2}m{v^{'}}_{\text{A}}^{\text{2}}+\dfrac{1}{2} \times 3m{v^{'}}_{\text{B}}^{2}$

解得$v'=-g\sqrt{\dfrac{2m}{k}}$，${v_{\text{B}}}'=g\sqrt{\dfrac{2m}{k}}$

由$x=A_{0}\sin\left( \sqrt{\dfrac{k}{m}}t \right)$，可知小球$A$上滑过程做简谐运动，小球$A$第一次速度为零时，距离达到最大值$x_{m}=A_{0}$，则有$\sqrt{\dfrac{k}{m}}t_{\text{A}}=\dfrac{\pi}{2}$

解得$t_{\text{A}}=\dfrac{\pi}{2}\sqrt{\dfrac{m}{k}}$

小球$B$碰撞后开始在直杆$OM$上做匀减速运动，加速度为$\mu g$，设小球$B$速度减为$0$所经历的时间为$t_{B}$，则$t_{\text{B}}=\dfrac{{v_{\text{B}}}'}{\mu g}=\dfrac{1}{\mu}\sqrt{\dfrac{2m}{k}}$

因$t_{B} \gt t_{A}$，则小球$A$在碰撞后第一次速度为零时，小球$B$与$O$点的距离为$s$，则有$s={v_{\text{B}}}'t_{\text{A}}-\dfrac{1}{2}\mu gt_{\text{A}}^{\text{2}}$

联立解得$s=\left( \dfrac{\sqrt{2}}{2}\pi-\dfrac{\sqrt{3}}{24}\pi^{2} \right)\dfrac{mg}{k}$