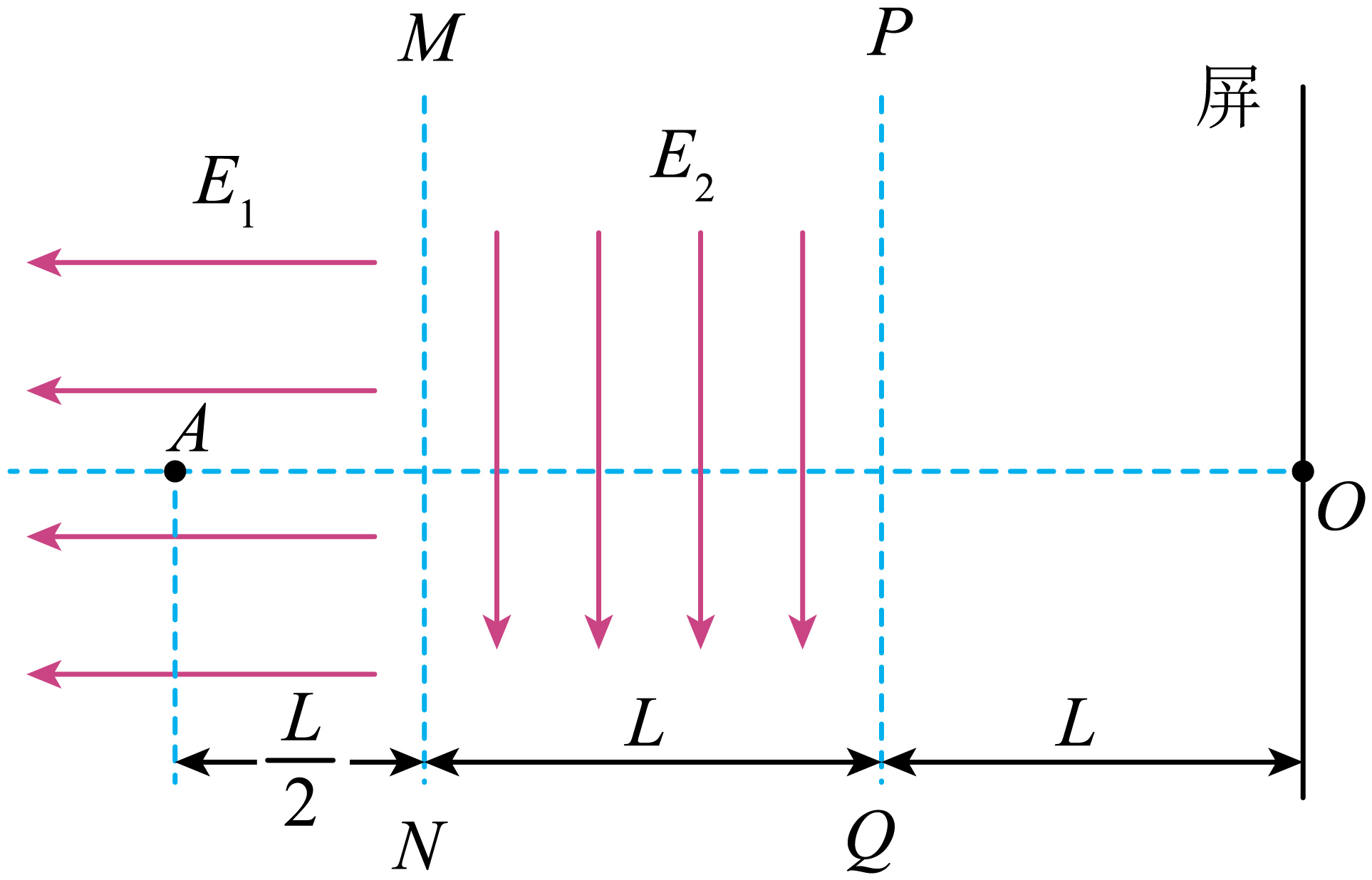
电子从释放到打到屏上所用的时间；

$3\\sqrt{\\dfrac{mL}{eE}}$

电子运动情况如图所示

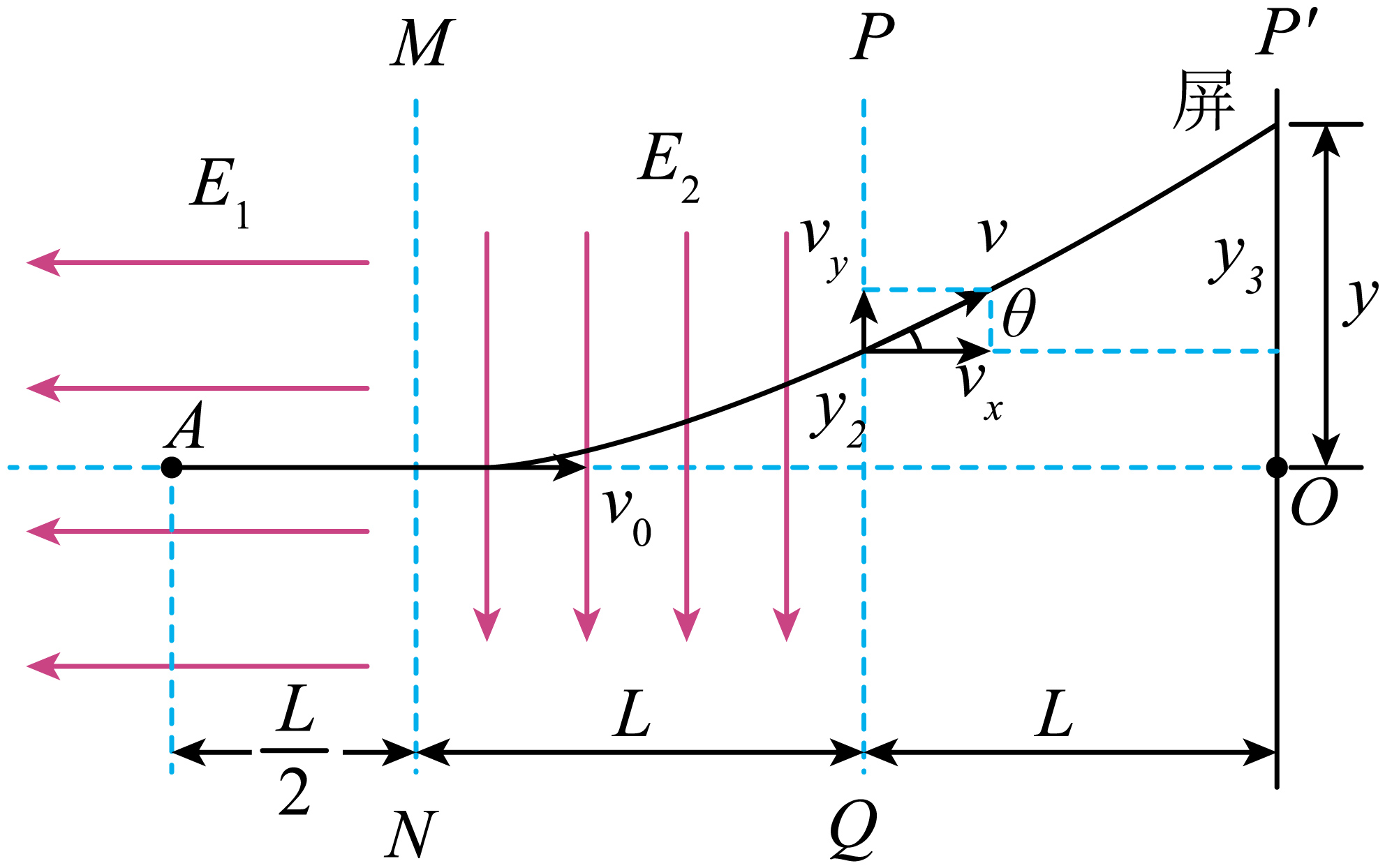
电子在电场$E_{1}$中做初速度为零的匀加速直线运动。设加速度为$a_{1}$，时间为$t_{1}$，由牛顿第二定律和运动学公式得 $a=\dfrac{eE_{1}}{m}=\dfrac{eE}{m}$，$\dfrac{L}{2}=\dfrac{1}{2}a{t_{1}}^{2}v_{0}=a_{1}t_{1}$

解得$v_{0}=\sqrt{\dfrac{eEL}{m}}$，$t_{1}=\sqrt{\dfrac{mL}{eE}}$

电子在$MN$右侧到屛的区域内，沿$AO$方向不受力，故沿$AO$方向的分运动为匀速直线运动，分速度$v_{x}=v_{0}=\sqrt{\dfrac{eEL}{m}}$

在该区域运动时间为$t'=\dfrac{2L}{v_{0}}=2\sqrt{\dfrac{mL}{eE}}$

电子从释放到打到屏上所用的时间$t=t_{1}+t'=3\sqrt{\dfrac{mL}{eE}}$

电子刚射出电场$E_{2}$时的速度方向与$AO$连线夹角$\theta$的正切值$\tan \theta$；

$2$

电子在电场$E_{2}$中受到与场强方向相反的电场力，做类平抛运动，沿$AO$方向的分运动为匀速直线运动，在电场$E_{2}$中运动的时间$t_{2}=\dfrac{L}{v_{0}}= \sqrt{\dfrac{mL}{eE}}$

沿垂直$AO$方向的分运动为匀加速直线运动，加速度为$a_{y}=\dfrac{eE_{2}}{m}=\dfrac{2eE}{m}$

电子刚射出电场$E_{2}$时，沿垂直$AO$方向的分速度为$v_{y}=a_{y}t_{2}=2\sqrt{\dfrac{eEL}{m}}$

则$\tan\theta=\dfrac{v_{y}}{v_{x}}=2$

电子打到屏上的点$P'$到点$O$的距离$y$。

$3L$

电子在电场$E_{2}$中沿垂直$AO$方向的分运动为匀加速直线运动，走过的分位移为$y_{2}=\dfrac{v_{y}}{2}t_{2}=L$

电子在虚线$PQ$右侧不受力，做匀速直线运动，该匀速直线运动沿$AO$方向的分运动为匀速直线运动，在该区域运动的时间$t_{3}=\dfrac{L}{v_{0}}=\sqrt{\dfrac{mL}{eE}}$

电子沿垂直$AO$方向的分运动为匀速直线运动，走过的分位移为 $y_{3}=v_{y}t_{3}=2L$

电子打到屏上的点$P'$到点$O$的距离为$y=y_{2}+y_{3}=3L$