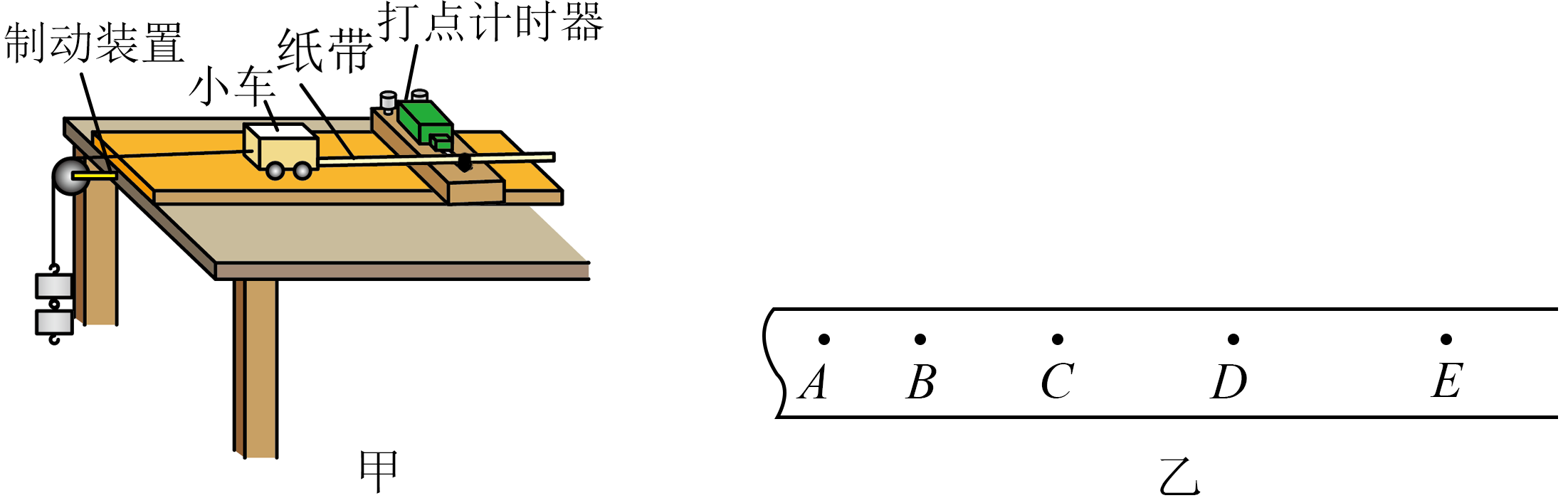
为补偿打点计时器对小车的阻力及其他阻力，可以使木板的一侧垫高，关于补偿阻力，下列操作最合理的一项是$(\quad\ \ \ \ )$。

未连接纸带前，放开小车，小车能由静止开始沿木板下滑

未连接纸带前，轻碰小车，小车能匀速稳定下滑

放开拖着纸带的小车，小车能由静止开始沿木板下滑

放开拖着纸带的小车，轻碰小车，小车能匀速稳定下滑

该实验需要平衡摩擦力，操作时可以使木板的一侧垫高，放开拖着纸带的小车，轻碰小车，使小车能匀速稳定下滑，

故选：$\rm D$。

某次实验时得到的纸带如图乙所示，$A$、$B$、$C$、$D$、$E$为选取的$5$个计数点，相邻两计数点之间还有$4$个点没有画出，用刻度尺测得相邻两计数点之间的距离分别为$x_{AB}=2.23\;\rm cm$、$x_{BC}=3.13\;\rm cm$、$x_{CD}=4.01\;\rm cm$、$x_{DE}=4.91\;\rm cm$。打点计时器所用交流电源的频率为$50\;\rm Hz$，则可得小车运动的加速度大小为                 $\;\rm m/s^2$（计算结果保留$2$位有效数字）。

打点计时器所用交流电源的频率为$50\;\rm Hz$，所以每个点之间的时间间隔为$\dfrac{1}{f}=0.02\;\rm \text{s}$

相邻两计数点之间还有$4$个点没有画出，故计数点间的时间间隔为$T=5 \times 0.02\;\rm s=0.1\;\rm s$

根据逐差公式可得$x_{CE}-x_{AC}=a(2T)^{2}$，代入数据解得$a=0.89\;\rm m/s^{2}$

在研究加速度与力的关系时，该同学根据实验数据作出的$a-F$图像如图丙所示，发现该图线不通过坐标原点且$BC$段明显偏离直线，分析其产生的原因，下列说法正确的是$(\quad\ \ \ \ )$。

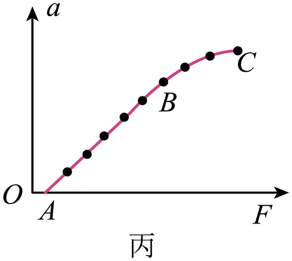
不通过坐标原点可能是因为平衡阻力不足

不通过坐标原点可能是因为平衡阻力过度

图线$BC$段弯曲可能是未满足钩码总质量远小于小车总质量的条件

图线$BC$段弯曲可能是未满足钩码总质量远大于小车总质量的条件

$\rm AB$．根据图像可知，当力$F$达到一定大小后，小车才开始运动，可知可能是平衡阻力不足，故$\rm A$正确，$\rm B$错误；

$\rm CD$．图线$BC$段弯曲可能是未满足钩码总质量远小于小车总质量的条件，这样小车受到的拉力不再等于钩码的重力，$a$和$F$不再成正比，故$\rm C$正确，$\rm D$错误。

故选：$\rm AC$。

实验中将钩码重力大小作为细绳对小车的拉力大小，在实验中引入了系统误差，考虑实际情况，细绳对小车的拉力$F$与钩码重力$mg$的大小关系应为$F$                 $mg$（填“$\gt $”“$\lt $”或“$=$”）；若实验中补偿阻力后，摩擦阻力的影响可忽略不计，某次实验时，钩码质量$m=30\;\rm g$，小车质量$M=250\;\rm g$，实验中因将钩码重力大小作为细绳对小车的拉力大小引入的百分误差$\delta=$                 $\%$。$($$\delta=\dfrac{\left| F-F_{真} \right|}{F_{真}} \times 100\text{\%}$，$F$为实验中处理数据时细绳的拉力值，$F_{真}$为细绳拉力的真实值。计算结果保留$2$位有效数字）

考虑实际情况，对钩码，根据牛顿第二定律$mg-T=ma$

对小车，根据牛顿第二定律$T=Ma$

联立可得$a=\dfrac{mg}{M+m}$，$T=\dfrac{Mmg}{M+m}$

可得$T=\dfrac{Mmg}{M+m}=\dfrac{M}{M+m}mg \lt mg$

钩码质量$m=30g$，小车质量$M$$=250g$，百分误差为$\delta=\dfrac{\left| F-F_{真} \right|}{F_{真}} \times 100\text{\%}$

其中$F$为实验中处理数据时细绳的拉力值，为$mg$

$F_{真}$为细绳拉力的真实值，为$T=\dfrac{Mmg}{M+m}=\dfrac{M}{M+m}mg$

可得$\delta=\dfrac{\left| F-F_{真} \right|}{F_{真}} \times 100\text{\%=}\dfrac{M+m}{M}-1$，解得$\delta=0.12=12\%$