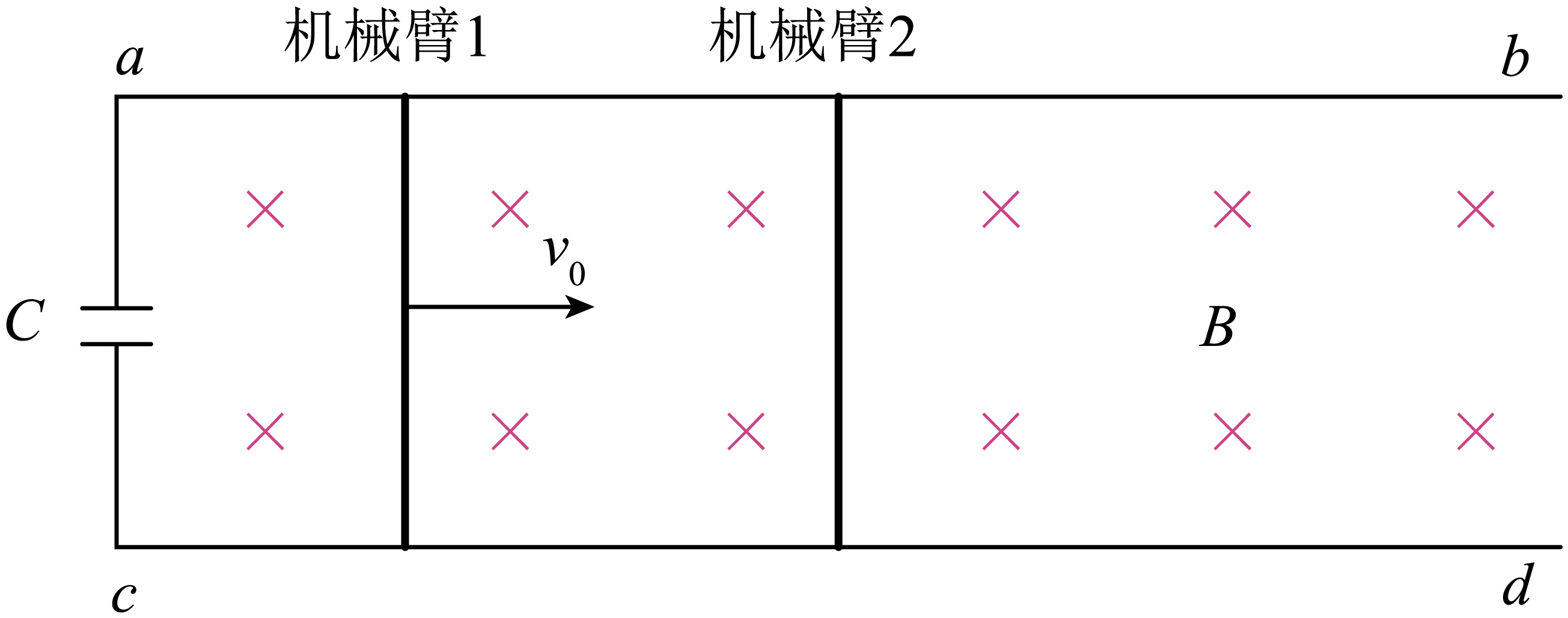
求初始时刻机械臂$1$的感应电动势大小和感应电流方向；

$BLv_{0}$，沿机械臂$1$向上

由法拉第电磁感应定律可知，初始时刻机械臂$1$的感应电动势大小为$E=BLv_{0}$

由右手定则可知感应电流方向沿机械臂$1$向上。

系统达到稳定状态前，若机械臂$1$和$2$中的电流分别为$I_{1}$和$I_{2}$，写出两机械臂各自所受安培力的大小；若电容器两端电压为$U$，写出电容器电荷量的表达式；

$BI_{1}L$，$BI_{2}L$，$Q=CU$

在达到稳定前，两机械臂电流分别为$I_{1}$和$I_{2}$，两机械臂安培力的大小分别为$F_{1}=BI_{1}L$，$F_{2}=BI_{2}L$

设电容器所带电荷量为$Q$，则$Q=CU$

求系统达到稳定状态后两机械臂的速度。若要两机械臂不相撞，二者在初始时刻的间距至少为多少？

$\\dfrac{mv_{0}}{CB^{2}L^{2}+ 2m}$，方向向右；$\\dfrac{mv_{0}R}{B^{2}L^{2}}$

达到稳定$I_{1}=I=0$时，两机械臂的速度相同，产生的感应电动势与电容器的电压相等，回路中没有电流结合（$2$）问的分析可知此时$I_{1}=I_{2}=0$，$U=\dfrac{BLmv_{0}}{2m+B^{2}L^{2}C}$

同时$U=BLv$

可得两机械臂的速度为$v=\dfrac{mv_{0}}{2m+B^{2}L^{2}C}$

方向向右

结合（$2$）问分析，在任意时刻有$U=BLv_{1} − I_{1}R=BLv_{2}+I_{2}R$

即$BL(v_{1} − v_{2})=I_{2}R+I_{1}R$

对该式两边取全过程时间的累计有$BL(v_{1} − v_{2})\Delta t=I_{2}R\Delta t+I_{1}R\Delta t$

其中$(v_{1} − v_{2})\Delta t=x_{1} − x_{2}=d_{\min}$，$I_{1}\Delta t=Q_{1}'$,$I_{2}\Delta t=Q_{2}'$

即$BLd_{\min}=(Q_{1}'+Q_{2}')R$

从开始到最终稳定的过程中，对机械臂$1$和机械臂$2$分别根据动量定理有

$-B\overline{I}_{1}'L\cdot\Delta t=mv-mv_{0}$，$B\overline{I}_{2}'L\cdot\Delta t=mv$

即$BLQ_{1}'=mv_{0}−mv$，$BLQ_{2}'=mv$

可得$BL(Q_{1}'+Q_{2}')=mv_{0}$

联立解得稳定时的速度和两棒间初始距离的最小值为$d_{\min}=\dfrac{mv_{0}R}{B^{2}L^{2}}$