高中 | 双棒模型 题目答案及解析
稿件来源:高途
高中 | 双棒模型题目答案及解析如下,仅供参考!
选修3-2
第四章 电磁感应
4.4 法拉第电磁感应定律
双棒模型
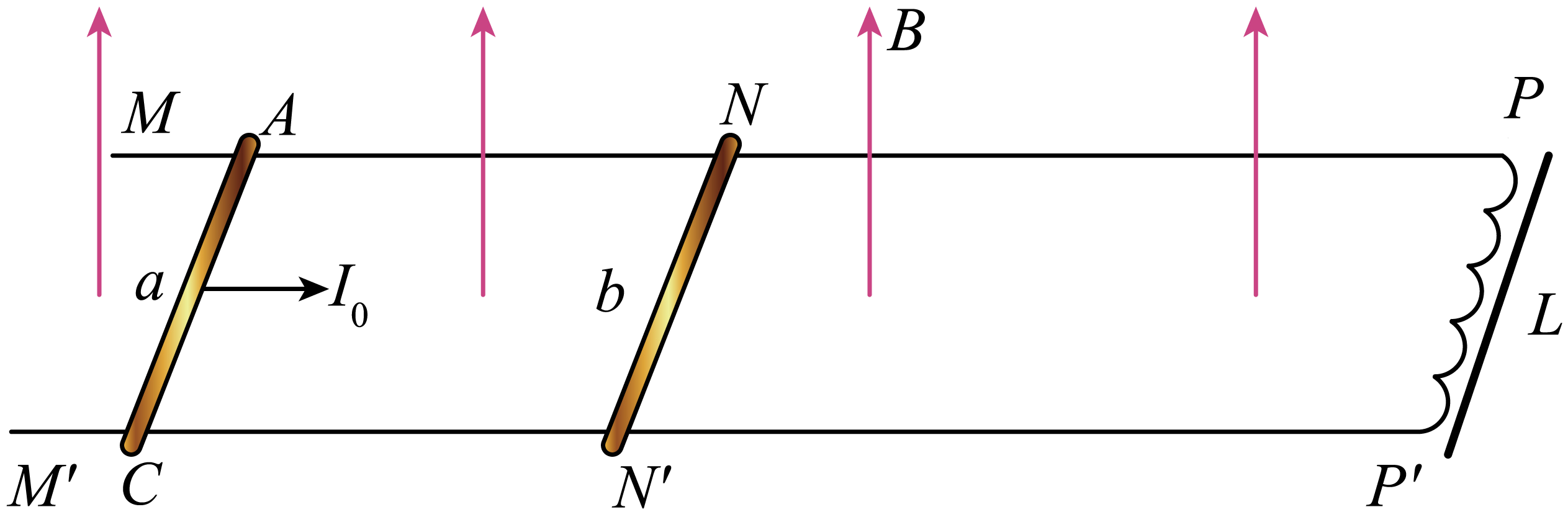
如图所示,粗糙水平导轨$MN$、$N'M'$和光滑水平导轨$NP$、$P'N'$在$NN'$处平滑连接,但彼此绝缘,导轨间距均为$d$,电阻均忽略不计;导轨右端$PP'$之间连接直流电阻不计的线圈,其自感系数为$L$,整个导轨处于竖直向上、磁感应强度为$B$的匀强磁场中。在导轨上垂直放置两根质量均为$m$,长度均为$d$的金属棒$a$和$b$,$a$棒电阻为$R$,$b$棒电阻不计。开始时$b$棒恰好处于导轨$MN$、$N'M'$的最右端且被锁定,$a$棒处于距离$NN'$为$d$处:现给$a$棒一个平行于导轨向右、大小为$I_{0}$瞬时冲量,当两棒即将碰撞时解除$b$棒的锁定,两棒之间发生弹性正碰,碰撞后瞬间$b$棒的速度为$v_{b}=\dfrac{I_{0}}{4m}$。知$a$棒与导轨$MN$、$N'M'$间的动摩擦因数为$\mu $,重力加速度为$g$,两棒碰撞时间极短。
金属棒$a$获得瞬时冲量$I_{0}$的电动势大小;
$E= \\dfrac{BdI_{0}}{m}$
"]]对$a$棒,根据动量定理有$I_{0}=mv_{a0}-0$
解得$v_{a0}=\dfrac{I_{0}}{m}$
此时$a$棒电动势$E=Bdv_{a0}=\dfrac{BdI_{0}}{m}$
$a$棒开始运动后,两棒经过多长时间发生第一次碰撞;
$\\Delta t=\\dfrac{3I_{0}R- 4B^{2}d^{3}}{4\\mu mgR}$
"]]根据$\mu mg\Delta t+I_{安}=mv_{a0} − mv_{a}$
其中$I_{安}=B{I}dt=Bqd=\dfrac{B^{2}d^{3}}{R}$
两棒碰撞时时间极短,故两棒组成系统动量守恒,且两棒之间为弹性碰撞。设碰前瞬间$a$棒速度为$v_{a}$,碰后瞬间$a$棒速度为$v'_{a}$,由动量守恒和机械能守恒有$mv_{a}=mv'_{a}+mv_{b}$,$\dfrac{1}{2}mv_{a}^{2}=\dfrac{1}{2}m{v'}_{a}^{2}+\dfrac{1}{2}mv_{b}^{2}$
解得$v_{a}=\dfrac{I_{0}}{4m}$,$v'_{a}=0$
联立解得$\Delta t=\dfrac{3I_{0}R-4B^{2}d^{3}}{4\mu mgR}$
求两棒碰撞前的过程中,$a$棒上产生的焦耳热:
$Q=\\dfrac{15I_{0}^{2}}{32m}-\\mu mgd$
"]]在两棒碰撞过程中,根据能量守恒定律有$\dfrac{1}{2}mv_{a0}^{2}-\dfrac{1}{2}mv_{a}^{2}=Q +\mu mgd$
由于$v_{a0}=\dfrac{I_{0}}{m}$,$v_{a}=\dfrac{I_{0}}{4m}$
解得$Q=\dfrac{15I_{0}^{2}}{32m}-\mu mgd$
已知$b$棒在导轨$NP$、$P'N'$上的运动是简谐运动的一部分,求$b$棒从滑上导轨$NP$、$P'N'$到再次回到$NN'$所用的时间。(提示:简谐运动的回复力与位移的关系为$F=-kX$,运动周期$T= 2\pi\sqrt{\dfrac{m}{k}}$,线圈产生的感应电动势$E=L\dfrac{\Delta I}{\Delta t}$。)
$t=\\dfrac{\\pi\\sqrt{mL}}{Bd}$
"]]当棒$b$滑上水平导轨后,其与线圈组成的回路无电阻,有$E_{v}=E_{L}$
在$\Delta t$时间内有$L\dfrac{\Delta i}{\Delta t}=Bdv_{1}=Bd\dfrac{\Delta x}{\Delta t}$
两边积分可得$i=\dfrac{Bd}{L}x$
故安培力$F=- Bid=- \dfrac{B^{2}d^{2}}{L}x$
故$k=\dfrac{B^{2}d^{2}}{L}$
故周期$T=2\pi\sqrt{\dfrac{m}{k}}=\dfrac{2\pi\sqrt{mL}}{Bd}$
棒$b$从$NN'$又回到$NN'$经过了半个周期,则有$t=\dfrac{1}{2}T=\dfrac{\pi\sqrt{mL}}{Bd}$
高中 | 双棒模型题目答案及解析(完整版)
