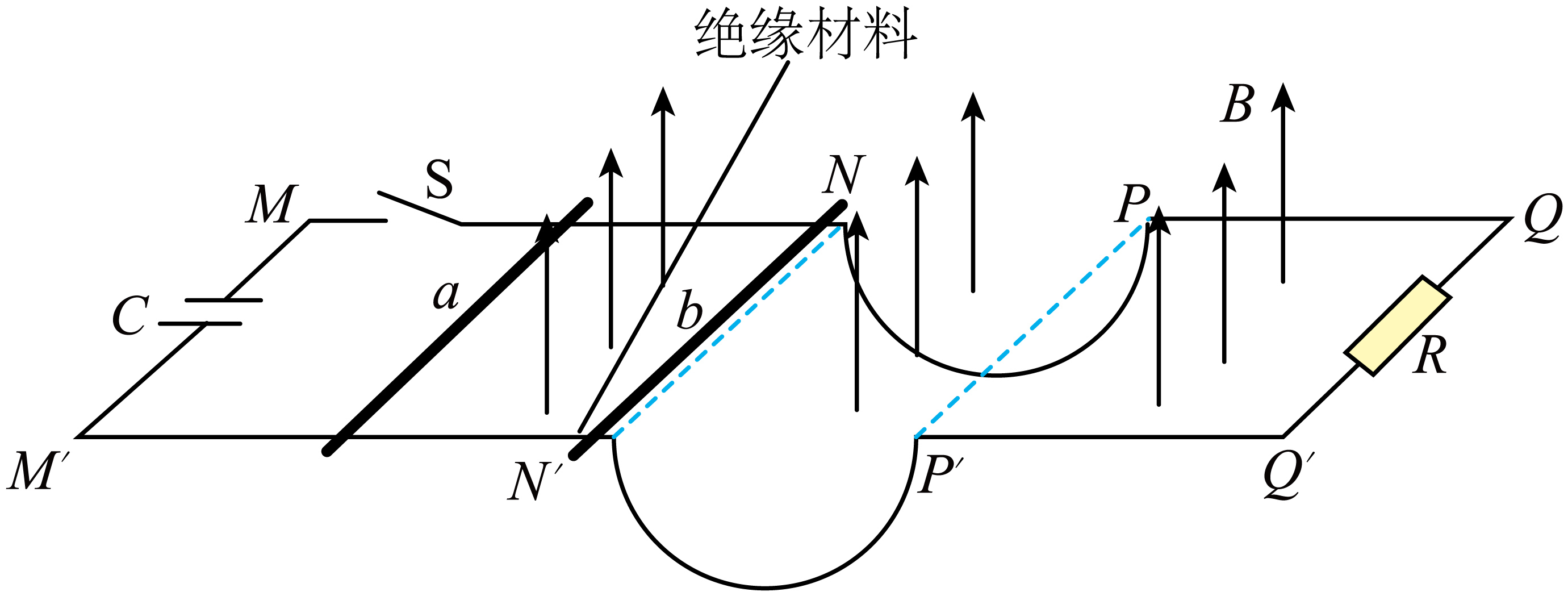
$b$棒运动到最低点回路中的感应电流大小；

$2\\;\\rm A$

$b$棒运动至最低点，由牛顿第二定律$F_{\text{N}}-mg= m\dfrac{v_{b}^{2}}{r}$

代入题中数据，解得$v_{b}=2\;\rm m/s$

则电流$I=\dfrac{E}{R}=\dfrac{BLv_{b}}{R}=2\;\rm \text{A}$

电容器初始时的电压$U_{0}$及弹射$a$棒释放的电荷量$q$；

$U_{0}=4\\;\\rm V$，$q=0.2\\;\\rm C$

质量相等的$a$、$b$棒发送弹性碰撞，速度互换，可知碰前$a$棒速度$v_{a}=v_{b}=2\;\rm m/s$，规定向右为正方向，对$a$棒，由动量定理有$∑BIL ⋅ \Delta t=m_{a}v_{a}$

因为$BIq=m_{a}v_{a}$

联立解得$q=0.2\;\rm C$

电容器释放电荷量与通过$a$棒的电荷量相等，则$q=C(U_{0}-U')$

$a$棒被弹射时运动距离足够长，可知$a$棒的电动势与电容器的电压相等，即$U'=BLv_{a}=2\;\rm V$

联立求得$U_{0}=4\;\rm V$

整个过程中$R$上产生的焦耳热。

$1.4\\;\\rm J$

$b$棒在圆弧运动时产生的感应电动势等效为正弦式交变电流，电动势有效值$E_{有}=\dfrac{E}{\sqrt{2}}= \sqrt{2}\;\rm \text{V}$

产生的焦耳热$Q_{1}=\dfrac{E_{有}^{2}}{R}t$

联立解得$Q_{1}=1.2\;\rm J$

撤去外力后，$b$棒的动能全部转化为焦耳热$Q_{2}=\dfrac{1}{2}m_{b}v_{b}^{2}=0.2\;\rm \text{J}$

故整个过程中$R$上产生的焦耳热$Q=Q_{1}+Q_{2}=1.4\;\rm J$