| 斜面问题 题目答案及解析
稿件来源:高途
| 斜面问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
斜面问题
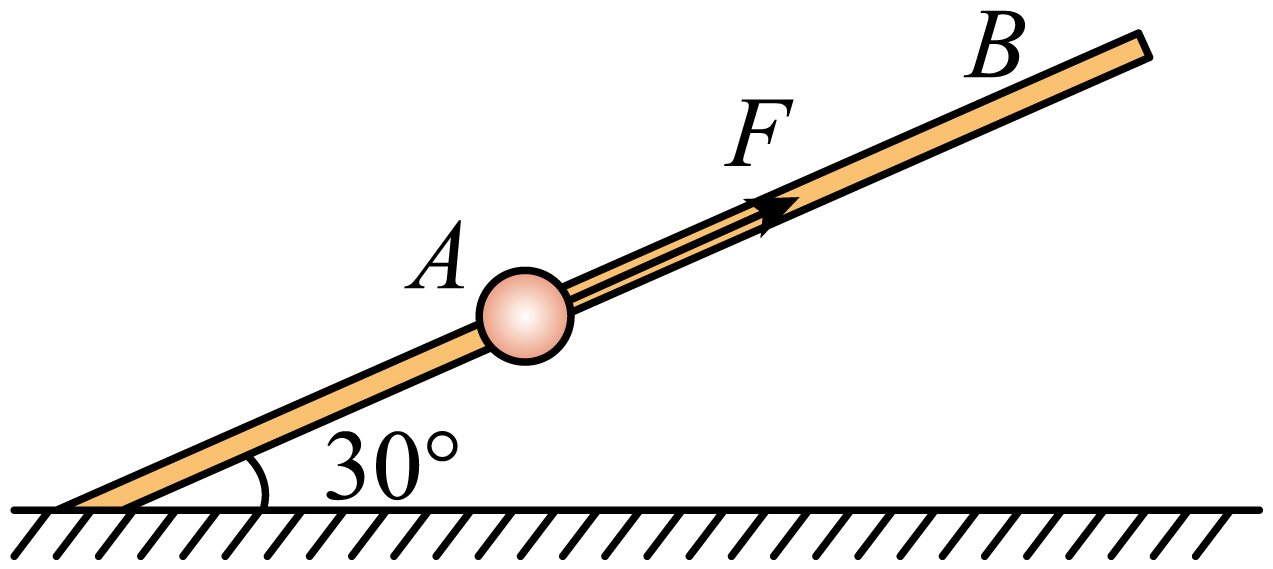
如图,一质量为$1\;\rm kg$的小球套在一根固定的直杆上,直杆与水平面夹角$\theta$为$30^\circ$,现小球在$F=10\;\rm N$的沿杆向上的拉力作用下,从$A$点静止出发沿杆向上运动。已知杆与球间的动摩擦因数为$\dfrac{\sqrt{3}}{5}$。求:
小球运动的加速度$a_{1}$;
$2\\;\\rm m/s^{2}$
"]]在力$F$作用时有$F-mg\sin 30^\circ -\mu mg\cos 30^\circ =ma_{1}$
代入数据解得$a_{1}=2\;\rm m/s^{2}$
若$F$作用$2\;\rm s$后撤去,小球上滑过程中距$A$点最大距离$s_{m}$。
$5\\;\\rm m$
"]]刚撤去$F$时,小球的速度$v_{1}=a_{1}t_{1}=4\;\rm m/s$
小球的位移$s_{1}=\dfrac{v_{1}}{2}t_{1}=4\;\rm \text{m}$
撤去力$F$后,小球上滑时有$mg\sin 30^\circ +\mu mg\cos 30^\circ =ma_{2}$
代入数据解得$a_{2}=8\;\rm m/s^{2}$
因此小球上滑时间$t_{2}=\dfrac{v_{1}}{a_{2}}=0.5\;\rm \text{s}$
上滑位移$s_{2}=\dfrac{v_{1}}{2}t_{2}=1\;\rm \text{m}$
则小球上滑的最大距离为$s_{m}=s_{1}+s_{2}=5\;\rm m$
| 斜面问题题目答案及解析(完整版)
