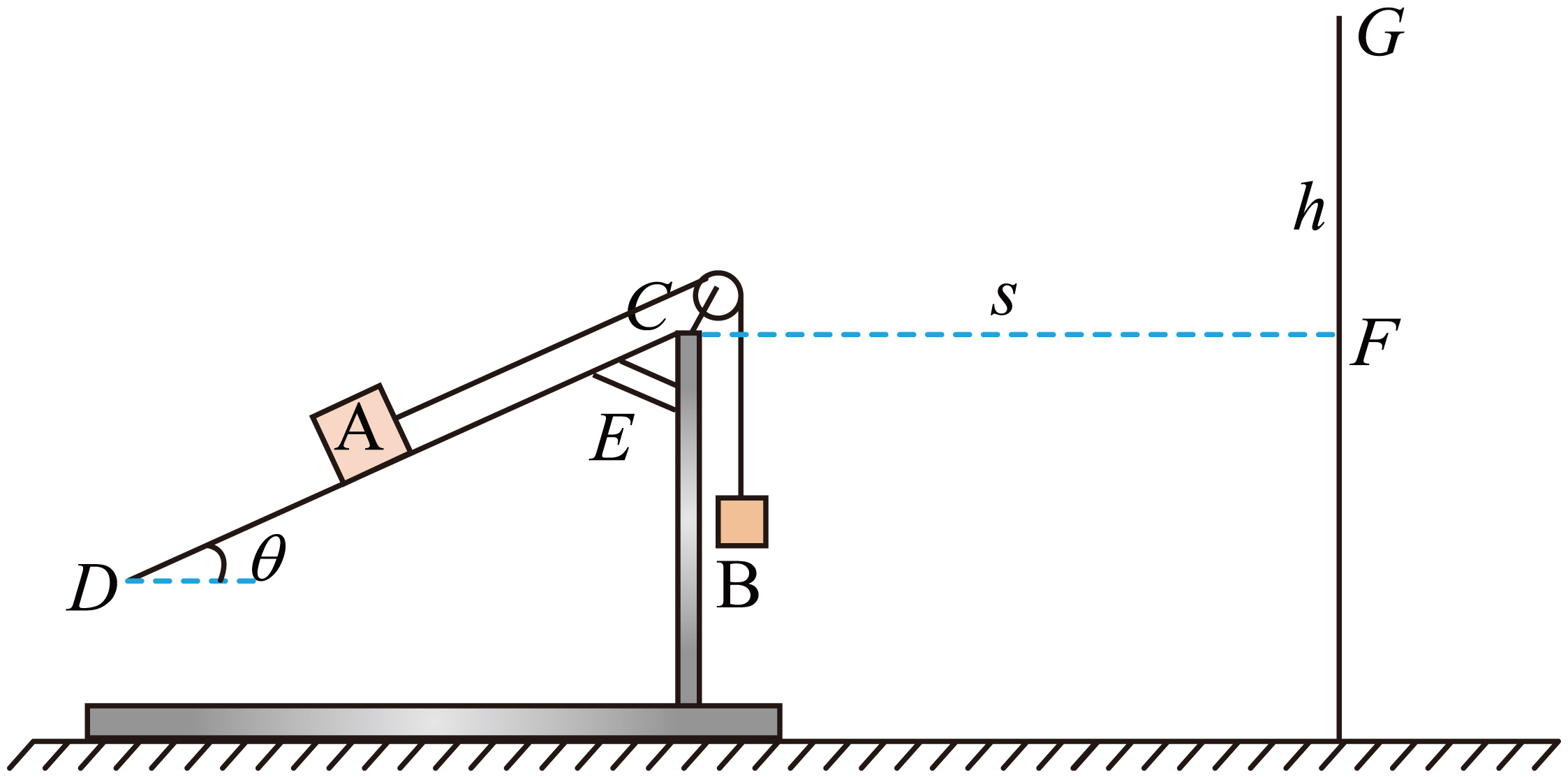
设定斜面倾角为$30^\circ $，将物块$A$单独放置于斜面上，$A$沿斜面下滑时装置未发生移动。求$A$沿斜面下滑的加速度大小。

$5\\;\\rm m/s^{2}$

对物块$A$受力分析，由牛顿第二定律$mg\sin \theta=ma_{1}$

解得$A$沿斜面下滑的加速度大小为$a_{1}=g\sin\theta=5\;\rm m/s^{2}$

设定斜面倾角为$37^\circ $，将质量均为$m=1\;\rm kg$两物块$A$、$B$用轻质细线连接后放置在斜面上（如图所示），细线拉直且$A$与滑轮间细线与斜面平行，然后同时由静止释放$A$和$B$。观察到$A$沿斜面向上匀加速运动过程中整个装置保持静止。假设最大静摩擦力等于滑动摩擦力。求装置底部与地面之间的动摩擦因数的范围。

$\\mu \\geqslant \\dfrac{4}{73}$

由题意可知$m_{A}=m_{B}=m=1\;\rm kg$

对两物块$A$、$B$整体由牛顿第二定律$m_{B}g-m_{A}g\sin37^\circ =(m_{A}+m_{B})a_{2}$

解得$a_{2}=2\;\rm m/s^{2}$

对两物块$A$、$B$和整个装置，整体水平方向有装置底部与地面之间的摩擦力大小为$f=m_{A}a_{2}\cos37^\circ =1.6\;\rm N$

竖直方向有$(m_{A}+m_{B}+M)g-N=m_{B}a_{2}-m_{A}a_{2}\sin37^\circ $

解得$N=29.2\;\rm N$

根据$f\leqslant \mu N$

代入数据解得装置底部与地面之间的动摩擦因数的范围为$\mu \geqslant\dfrac{4}{73}$

现在将装置固定在地面上，斜面倾角可按需调节，换用新的$A$、$B$物块，重复（$2$）问操作，当$A$运动到$C$点前一瞬间，装置将自动收起定滑轮并切断细线，$B$离底座足够高。求要使$A$能够飞过挡板，$A$离开$C$点时速度的最小值及此情况下$A$在斜面上经历了多长的加速距离（本问中$m_{\text{A}}=\sqrt{3}\;\rm \text{kg}$，$m_{\text{B}}= 3\;\rm \text{kg}$）。

$\\sqrt{30}\\;\\rm \\text{m}/\\text{s}$，$(3+\\sqrt{3}\\text{)m}$

设物块$A$运动到$C$点时的速度大小为$v_{0}$，将$C$点时的速度分解为$v_{x}=v_{0}\cos\theta$，$v_{y}=v_{0}\sin\theta$

当物块$A$运动越过挡板位置时，水平方向由匀速直线运动，有$s=v_{0}\cos\theta t$

竖直方向由竖直上抛运动$H=v_{0}\sin\theta t-\dfrac{1}{2}gt^{2}$

联立解得$v_{0}=\sqrt{\dfrac{15}{\cos^{2}\theta\left( \sqrt{3}\tan\theta-H \right)}}$

令$y=\cos^{2}\theta\left( \sqrt{3}\tan\theta-H \right)=\dfrac{\sqrt{3}\sin2\theta-H\cos2\theta-H}{2}=\dfrac{\sqrt{3+H^{2}}\sin(2\theta-\alpha)-H}{2}$

由题意$H\geqslant 1$，且$\tan\alpha=\dfrac{H}{\sqrt{3}}$，则$\alpha\geqslant 30^\circ $

由$0^\circ\lt\theta\lt 90^\circ $，则$\sin(2\theta-\alpha)$最大值为$1$

即$y=\dfrac{\sqrt{3+H^{2}}-H}{2}=\dfrac{3}{2\left( \sqrt{3+H^{2}}+H \right)}$

则$H$增大，$y$减小，当$H=h=1\;\rm m$，$\theta=60^\circ $时，$y_{\max}=\dfrac{1}{2}$

则$v_{0\min}=\sqrt{30}\;\rm \text{m/s}$

此时$a_{3}=\dfrac{m_{\text{B}}g-m_{\text{A}}g\sin60{^\circ}}{m_{\text{A}}+m_{\text{B}}}=\dfrac{15-5\sqrt{3}}{2}\;\text{m/s}^{\text{2}}$

由运动学公式可得在此情况下$A$在斜面上经历的加速距离为$x=\dfrac{v_{0\min}^{2}}{2a_{{3}}}=(3+\sqrt{3})\;\rm \text{m}$