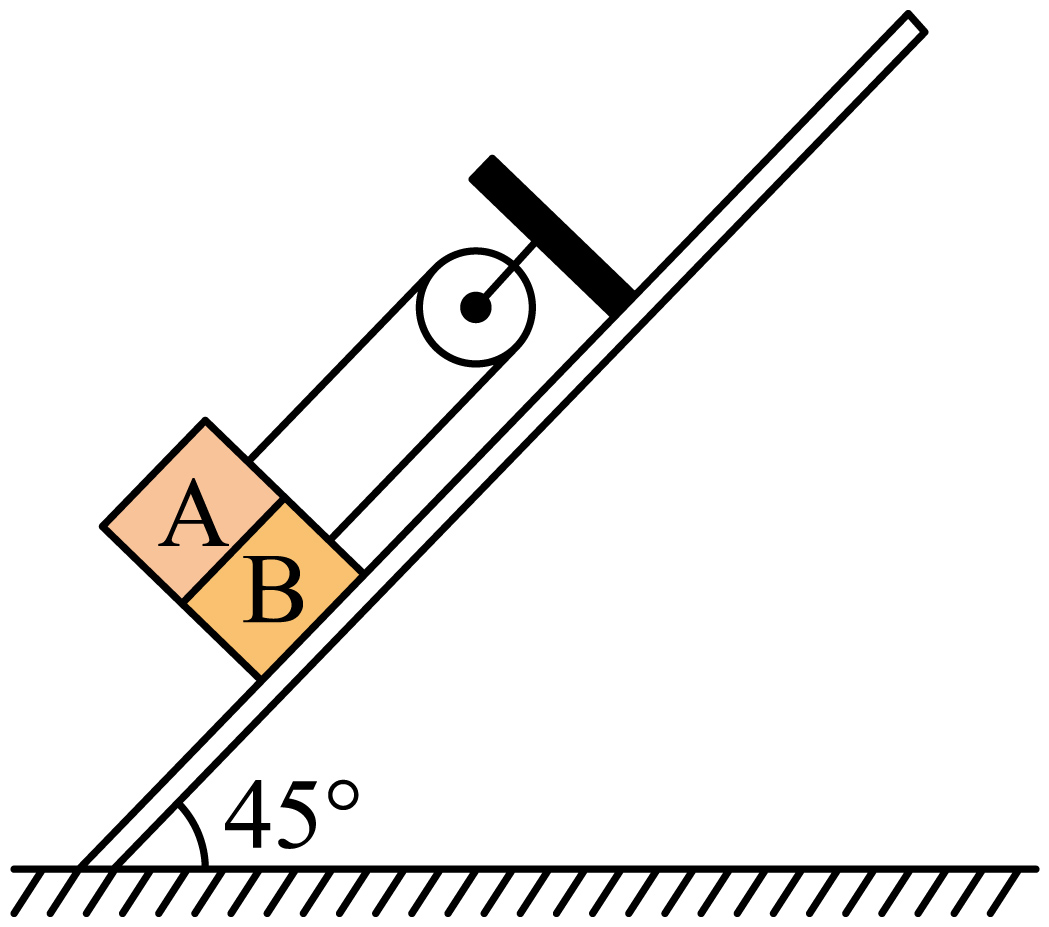
求倾斜木板对物块$B$的支持力大小；

$F=2\\sqrt{2}mg$； 

对物块$A$、$B$整体受力分析有$F=4mg\cos45^\circ $

$F=2\sqrt{2}mg$；

若物块$A$恰好不向下滑动，求物块$A$与$B$间的动摩擦因数；

$\\mu =0.2$；

当物块$A$恰好不下滑时，此时物块$B$恰好不上滑，设$A$、$B$间的弹力大小为$F_{N1}$，$B$与斜面间的弹力大小为$F_{N2}$，对物块$A$受力分析，得

沿斜面方向受力平衡有$3mg\sin 45^\circ =\mu F_{N1}+T$

垂直斜面方向受力平衡有$F_{N1}=3mg\cos 45^\circ $

对物块$B$受力分析，得

沿斜面方向受力平衡有$mg\sin 45^\circ +\mu F_{N1}+\mu F_{N2}=T$

垂直斜面方向受力平衡有$mg\cos 45^\circ +F_{N1}=F_{N2}$

联立解得$\mu =0.2$；

若对物块$A$施加平行轻绳的力$F$，要使物块$A$、$B$都静止，接触面间动摩擦因数为$\mu $，求$F$的最大值$F_\rm{m}$与$\mu $的函数关系。

当$\\mu \\lt \\dfrac{1}{7}$时，$F_{\\rm{m1}}=\\sqrt{2}mg(1+ 5\\mu)$；当$\\dfrac{1}{7} \\leqslant \\mu \\lt \\dfrac{5}{7}$时，$F_{\\rm{m2}}= \\dfrac{3\\sqrt{2}}{2}(\\mu+1)mg$；当$\\mu =\\dfrac{5}{7}$时，$F_{\\rm{m2}}= \\dfrac{3\\sqrt{2}}{2}(\\mu+1)mg$或$F_{\\rm{m3}}=\\sqrt{2}(5\\mu- 1)mg$；当$\\mu \\gt \\dfrac{5}{7}$时，$F_{\\rm{m3}}= \\sqrt{2}(5\\mu-1)mg$。

当动摩擦因数较小时，最大的力$F_\rm{m1}$为沿斜面向上推物块$A$时且物块$A$恰好不上滑物块$B$恰好不下滑。对物块$A$经受力分析沿斜面方向受力平衡有$F_{\rm m1}+T'=3mg\sin 45^\circ+\mu F_{N1}$

对物块$B$经受力分析沿斜面方向受力平衡有$T'+\mu F_{N1}+\mu F_{N2}=mg\sin 45^\circ$

其中$F_{N1}=3mg\cos 45^\circ$

$F_{N2}=4mg\cos 45^\circ$

联立解得$F_{\rm{m1}}=\sqrt{2}mg(1+5\mu)$

当动摩擦因数较大，$F$沿木板向上推物块$A$时$A$恰不上滑，物块$B$不向下滑动且细绳弯曲，对$B$受力分析沿斜面方向受力平衡有$\mu F_{N1}+f_{斜}=mg\sin45^\circ $

$f_{斜} \leqslant f_{斜\max}$

$f_{斜\max}=4\mu mg\cos45^\circ $

解得$\mu \geqslant \dfrac{1}{7}$

其中一种情况是$F_\rm{m2}$沿斜面向上推物块$A$时且物块$A$恰好不上滑，物块$B$不动且细绳弯曲。对$A$此时受力分析沿斜面方向受力平衡得$F_{\rm m2}=\mu F_{N1}+3mg\sin45^\circ $

得$F_{\rm m2}=\dfrac{3\sqrt{2}}{2}(\mu+1)mg$

一种情况是$F_\rm{m3}$沿斜面向下推物块$A$时且物块$A$恰好不下滑，物块$B$恰好不上滑。分别对$A$、$B$受力分析沿斜面方向均受力平衡有$F_{\rm m3}+3mg\sin 45^\circ=T+\mu F_{N1}$

$mg\sin 45^\circ+\mu F_{N1}+f_{斜}=T$

其中$f_{斜}=4\mu mg\cos45^\circ $

得$F_{\rm m3}=\sqrt{2}(5\mu-1)mg$

若$F_{\rm m3} \gt F_{\rm m2}$

则有$\mu \gt \dfrac{5}{7}$

综上分析：当$\mu \lt \dfrac{1}{7}$时，最大值为$F_{\rm{m1}}=\sqrt{2}mg(1+5\mu)$

当$\dfrac{1}{7} \leqslant \mu \lt \dfrac{5}{7}$时，最大值为$F_{\rm{m2}}=\dfrac{3\sqrt{2}}{2}(\mu+1)mg$

当$\mu=\dfrac{5}{7}$时，最大值为

$F_{\rm{m2}}=\dfrac{3\sqrt{2}}{2}(\mu+1)mg$或$F_{\rm{m3}}=\sqrt{2}(5\mu-1)mg$

当$\mu \gt \dfrac{5}{7}$时，最大值为$F_{\rm{m3}}=\sqrt{2}(5\mu-1)mg$。