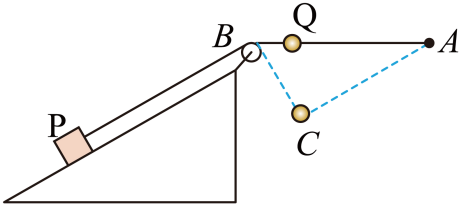
如图所示，倾角为$30^\circ $的光滑斜面固定在水平面上，斜面顶端$B$固定有轻质滑轮，轻绳左右两端分别连接质量均为$m$的物块$P$和小球$Q$，并跨过滑轮。小球$Q$还连接另一根长度为$4L$的轻绳。此轻绳另一端固定在$A$点，连接小球$Q$两端的绳一开始刚好拉直且水平，$AB$距离为$5L$。静止释放小球$Q$，到达$C$位置时，$BC$距离为$3L$，已知$\sin 37^\circ =0.6$，$\cos 37^\circ =0.8$，重力加速度为$g$。小球由静止释放运动到$C$位置的过程中，则$(\qquad)$

运动过程中物块与小球的速度大小始终相等

小球$Q$运动到$C$位置时，其速度大于物块的速度

小球$Q$运动到$C$位置的速度大小为$\\sqrt{\\dfrac{7}{5}gL}$

小球运动到$C$位置时，$A$点受力大小为$\\dfrac{9}{5}mg$

$\rm AB$．小球围绕$A$做圆周运动，速度方向垂直$AC$，根据关联速度分析方法，只有当$BC$与$AC$垂直时，小球的速度等于$BC$绳的速度，即等于物块$P$的速度，故$\rm AB$错误；

$\rm C$．小球运动到$C$位置，有$v_{P}=v_{Q}$

又根据机械能守恒定律有$mg \cdot \dfrac{12}{5}L-mg(3L-L)\sin 30{^\circ}=\dfrac{1}{2}mv_{{P}}^{2}+\dfrac{1}{2}mv_{{Q}}^{2}$

继而解得$v_{{Q}}=\sqrt{\dfrac{7}{5}gL}$，故$\rm C$正确；

$\rm D$．在$C$点，有$F-\dfrac{3}{5}mg=m\dfrac{v_{{Q}}^{2}}{4L}$

解得$F=\dfrac{19}{20}mg$，故$\rm D$错误。

故选：$\rm C$。