| 斜面问题 题目答案及解析
稿件来源:高途
| 斜面问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
斜面问题
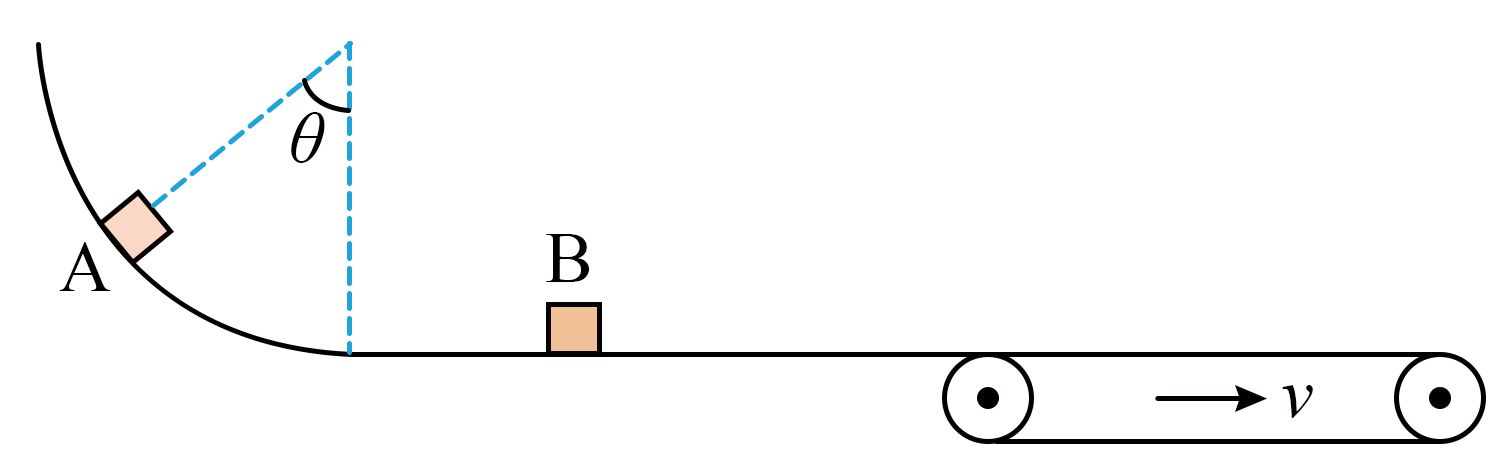
足够长的传送带固定在竖直平面内,半径$R=2\;\rm m$,圆心角$\theta=53^\circ $的圆弧轨道与平台平滑连接,平台与顺时针匀速转动的水平传送带平滑连接,工件$A$从圆弧顶点无初速度下滑,在平台与$B$发生弹性碰撞,已知$m_{A}=1\;\rm kg$,$m_{B}=4\;\rm kg$,$A$、$B$可视为质点,$A$、$B$与传送带间的动摩擦因数恒定,在传送带上运动的过程中,$B$物块因摩擦生热$Q=2\;\rm J$,忽略轨道及平台的摩擦,$g=10\;\rm m/s^{2}$,$\sin 53^\circ =0.8$,$\cos 53^\circ =0.6$。
求$A$滑到圆弧最低点时受到的支持力;
$18\\;\\rm N$,方向竖直向上
"]]$A$从开始到圆弧最低点过程,根据机械能守恒可得$m_{\text{A}}g\left( R-R\cos 53{^\circ} \right)= \dfrac{1}{2}m_{\text{A}}v_{0}^{2}$
解得$v_{0}=4\;\rm m/s$
在最低点根据牛顿第二定律得$F_{\text{N}}-m_{\text{A}}g=m_{\text{A}}\dfrac{v_{0}^{2}}{R}$
解得$F_{\rm N}=18\;\rm N$
方向竖直向上。
求$A$与$B$碰撞后各自的速度;
$A$的速度大小$2.4\\;\\rm m/s$,方向向左;$B$的速度大小$1.6\\;\\rm m/s$,方向向右
"]]$A$与$B$发生弹性碰撞,根据系统动量守恒可得$m_{\rm A}v_{0}=m_{\rm A}v_{\rm A}+m_{\rm B}v_{\rm B}$
根据系统机械能守恒可得$\dfrac{1}{2}m_{\text{A}}v_{0}^{2}=\dfrac{1}{2}m_{\text{A}}v_{\text{A}}^{2}+\dfrac{1}{2}m_{\text{B}}v_{\text{B}}^{2}$
联立解得$v_{\rm A}=-2.4\;\rm m/s$,$v_{\rm B}=1.6\;\rm m/s$
可知碰撞后$A$的速度大小$2.4\;\rm m/s$,方向向左;$B$的速度大小$1.6\;\rm m/s$,方向向右。
求传送带的速度以及$A$物块在传送带上运动的过程中因摩擦产生的热量。
答案见解析
"]]第一种情况,当传送带速度$v$小于$v_{B}$时,$B$滑上传送带后先减速后匀速运动;设$B$与传送带间的动摩擦因数为$\mu $,经过时间$t_{1}$后$B$与传送带共速,该段时间内$B$运动的位移为$x_{\text{B}}=\dfrac{v+ v_{\text{B}}}{2}t_{1}$
$B$与传送带的相对位移$\Delta x_{\text{B}}=x_{\text{B}}-vt_{1}=\dfrac{v_{\text{B}}-v}{2}t_{1}$
$B$物块因摩擦生热为$Q=\mu m_{\rm B}g ⋅ \Delta x_{\rm B}=2\;\rm J$
对$B$用动能定理可得$- \mu m_{\text{B}}gx_{\text{B}}=\dfrac{1}{2}m_{\text{B}}v^{2}-\dfrac{1}{2}m_{\text{B}}v_{\text{B}}^{2}$
联立解得$v=0.6\;\rm m/s$,另一解大于$v_{B}$舍去;
当$A$滑上传送带时,$v$小于$|v_{\rm A}|$,设经过时间$t_{2}$后$A$与传送带共速,该段时间内,$A$运动的位移为$x_{\text{A}}=\dfrac{v+\left| v_{\text{A}} \right|}{2}t_{2}$
$A$与传送带的相对位移$\Delta x_{\text{A}}=x_{\text{A}}-vt_{2}=\dfrac{\left| v_{\text{A}} \right|-v}{2}t_{2}$
$A$、$B$物块在传送带上做减速运动时的加速度相同,故$t_{2}:t_{1}=(|v_{\rm A}|-v):(v_{\rm B}-v)$
联立以上各式解得$\Delta x_{\rm A}:\Delta x_{\rm B}=81:25$
$A$物块因摩擦产生的热量$Q'=\mu m_{\rm A}g ⋅ \Delta x_{\rm A}$
联立解得$Q'=1.62\;\rm J$
第二种情况,当传送带速度$v$大于$v_{B}$时,$B$滑上传送带后先加速后匀速运动,设$B$与传送带间的动摩擦因数为$\mu '$,经过时间$t'_{1}$后$B$与传送带共速,该段时间内$B$运动的位移为${x'}_{\text{B}}=\dfrac{v_{\text{B}}+v}{2}{t'}_{1}$
$B$与传送带的相对位移$\Delta x'_{\text{B}}=vt'_{1}-x'_{\text{B}}=\dfrac{v-v_{\text{B}}}{2}t'_{1}$
$B$物块因摩擦生热为$Q=\mu 'm_{B}g ⋅ \Delta x'_{B}=2\;\rm J$
对$B$用动能定理可得$\mu'm_{\text{B}}gx'_{\text{B}}=\dfrac{1}{2}m_{\text{B}}v^{2}-\dfrac{1}{2}m_{\text{B}}v_{\text{B}}^{2}$
联立解得$v=2.6\;\rm m/s$,另一解小于$v_{B}$舍去;
当$A$滑上传送带时,$v$大于$|v_{A}|$,设经过时间$t'_{2}$后$A$与传送带共速,该段时间内,$A$运动的位移为$x'_{\text{A}}=\dfrac{\left| v_{\text{A}} \right|+v}{2}{t'}_{2}$
$A$与传送带的相对位移$\Delta x'_{\text{A}}=vt_{2}-x'_{\text{A}}=\dfrac{v-\left| v_{\text{A}} \right|}{2}t'_{2}$
$A$、$B$物块在传送带上做加速运动时的加速度相同,故$t'_{2}:t'_{1}=(v-|v_{\rm A}|):(v-v_{\rm B})$
联立以上各式解得$\Delta x'_{\rm A}:\Delta x'_{\rm B}=1:25$
$A$物块因摩擦产生的热量$Q''=\mu 'm_{\rm A}g ⋅ \Delta x'_{\rm A}$
联立解得$Q''=0.02\;\rm J$
| 斜面问题题目答案及解析(完整版)
