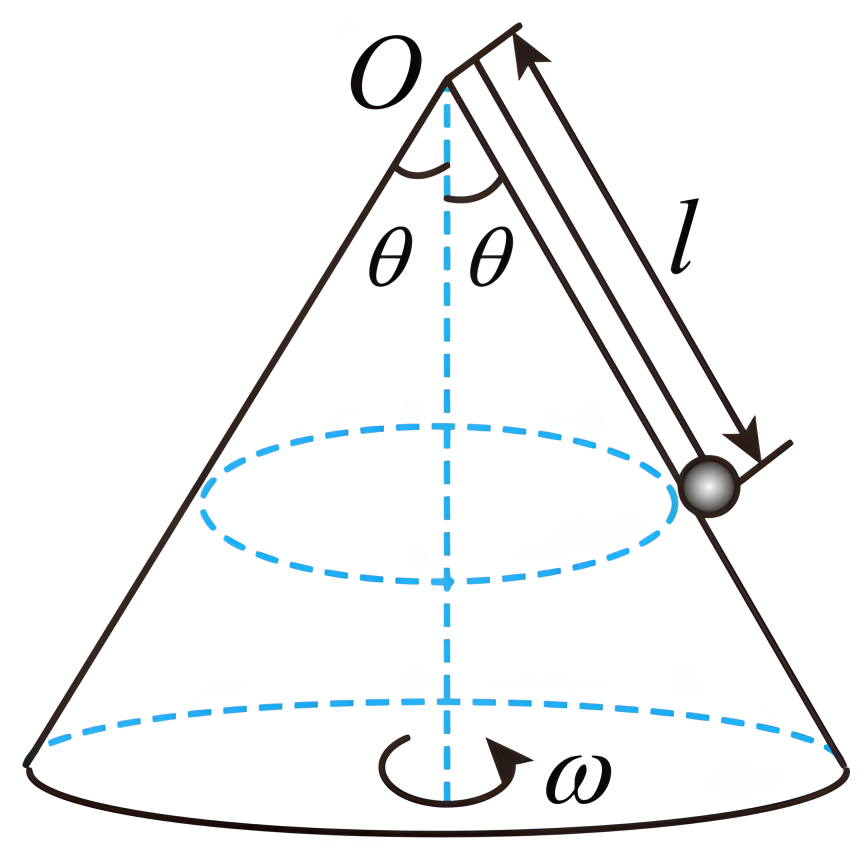
若细线与竖直方向的夹角为$60^\circ $，则小球的角速度$\omega_{1}$为多大；

$2\\sqrt{5}\\;\\rm \\text{rad/s}$

对小球，由牛顿第二定律得$mg\tan 60^\circ =m\omega_{1}^{2}l\sin 60^\circ $

代入数据解得$\omega_{1}=2\sqrt{5}\;\rm rad/s$

若（$1$）中小球在转动中绳子突然断裂，求小球落点到$O$在水平面投影的距离$s$；

$\\dfrac{\\sqrt{15}}{2}\\;\\rm \\text{m}$

绳子断裂后小球做平抛运动，竖直方向$h- l\cos 60{^\circ}=\dfrac{1}{2}gt^{2}$

水平方向$x=\omega_{1}l\sin 60^\circ \times t$

由几何知识得$s=\sqrt{x^{2}+\left( l\sin 60{^\circ} \right)^{2}}$

代入数据解得$s=\dfrac{\sqrt{15}}{2}\;\rm m$

若小球角速度$\omega_{2}=2\;\rm rad/s$，求细绳对小球的拉力大小。

$\\dfrac{236}{25}\\;\\rm \\text{N}$

小球恰好开始离开圆锥体时，由牛顿第二定律得$mg\tan 37^\circ =m\omega_{临}^{2}l\sin 37^\circ $

代入数据解得$\omega_{临}=\dfrac{5\sqrt{2}}{2}\;{\rm rad/s}\gt \omega_{2}=2\;\rm rad/s$

小球靠在圆锥体上做匀速圆周运动，在竖直方向，由平衡条件得$T\cos 37^\circ +F\sin 37^\circ =mg$

在水平方向，由牛顿第二定律得$T\sin 37^\circ-F\cos 37^\circ =m\omega_{2}^{2}l\sin 37^\circ $

代入数据解得$T=\dfrac{236}{25}\ \text{N}$