在元素周期表中，$\text{Fe}$位于第                周期                族。基态$\text{Fe}$原子与基态$\text{F}{{\text{e}}^{3+}}$离子未成对电子数之比为                。

四；$\\rm VIII$；$\\rm 4: 5$

$\rm Fe$为$\rm 26$号元素，位于元素周期表中第四周期$\rm VIII$族；基态$\rm Fe$原子电子排布式为$\rm [Ar]3d^{6}4s^{2}$，未成对电子数为$\rm 4$，基态$\rm Fe^{3+}$电子排布式为$\rm [Ar]3d^{5}$，未成对电子数为$\rm 5$；

尿素分子$\left( {{\text{H}}_{2}}\text{NCON}{{\text{H}}_{2}} \right)$与$\text{F}{{\text{e}}^{3+}}$形成配离子的硝酸盐$\left[ \text{Fe}{{\left( {{\text{H}}_{2}}\text{NCON}{{\text{H}}_{2}} \right)}_{6}} \right]{{\left( \text{N}{{\text{O}}_{3}} \right)}_{3}}$俗称尿素铁，既可作铁肥，又可作缓释氮肥。

①元素$\rm C$、$\rm N$、$\rm O$中，第一电离能最大的是                ，电负性最大的是                。

②尿素分子中，$\rm C$原子采取的轨道杂化方式为                。

③八面体配离子${{\left[ \text{Fe}{{\left( {{\text{H}}_{2}}\text{NCON}{{\text{H}}_{2}} \right)}_{6}} \right]}^{3+}}$中$\text{F}{{\text{e}}^{3+}}$的配位数为$\rm 6$，碳氮键的键长均相等，则与$\text{F}{{\text{e}}^{3+}}$配位的原子是                $\rm ($填元素符号$\rm )$。

$\\rm N$；$\\rm O$；$\\rm sp^{2}$；$\\rm O$

①同周期元素从左到右，第一电离能呈增大趋势，但$\rm N$原子$\rm 2p$轨道为半充满稳定结构，第一电离能：$\rm N\gt O\gt C$；同周期元素从左到右，电负性逐渐增大，因此电负性：$\rm O\gt N\gt C$；

②尿素分子$\left( {{\text{H}}_{2}}\text{NCON}{{\text{H}}_{2}} \right)$中$\rm C$原子形成$\rm 3$个$\rm \sigma$键，无孤电子对，采取的轨道杂化方式为$\rm sp^{2}$杂化。

③八面体配离子${{\left[ \text{Fe}{{\left( {{\text{H}}_{2}}\text{NCON}{{\text{H}}_{2}} \right)}_{6}} \right]}^{3+}}$中$\text{F}{{\text{e}}^{3+}}$的配位数为$\rm 6$，碳氮键的键长均相等，因此$\rm N$原子不会参与形成配位键，说明$\rm C=O$中$\rm O$原子参与配位，所以与$\text{F}{{\text{e}}^{3+}}$配位的原子是$\rm O$。

$\alpha -\text{Fe}$可用作合成氨催化剂、其体心立方晶胞如图所示$\rm ($晶胞边长为$ {a\;\rm pm} )$。

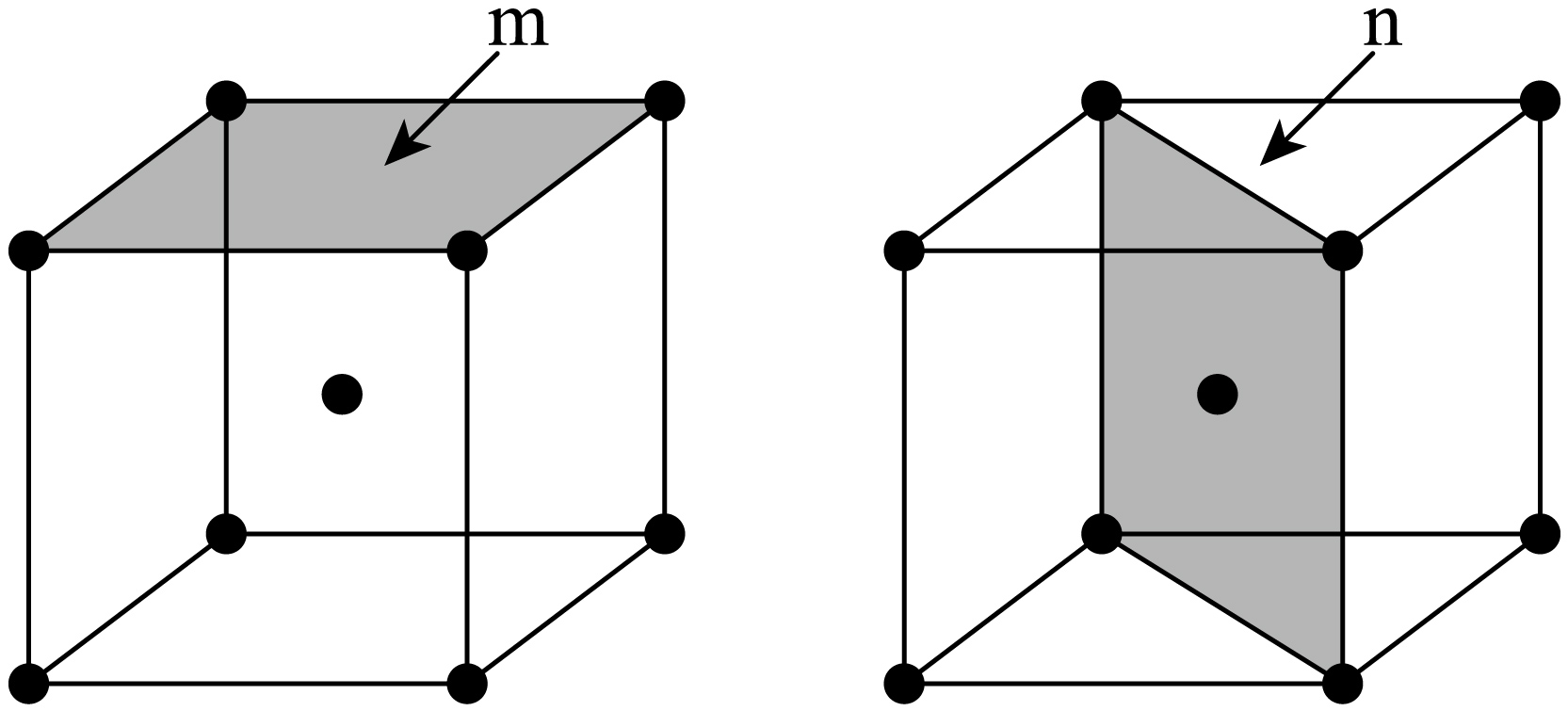
①$\rm \alpha-\text{Fe}$晶胞中$\rm \text{Fe}$原子的半径为                $\rm pm$。

②研究发现，$\rm \alpha-\text{Fe}$晶胞中阴影所示$\rm m$，$\rm n$两个截面的催化活性不同，截面单位面积含有$\rm \text{Fe}$原子个数越多，催化活性越低。$\rm m$，$\rm n$截面中，催化活性较低的是                ，该截面单位面积含有的$\rm \text{Fe}$原子为                个$\rm \cdot \text{p}{{\text{m}}^{-2}}$。

$\\dfrac{\\sqrt{3}{a}}{4}$；$\\rm n$；$\\dfrac{3\\sqrt{2}}{{4}{{{a}}^{2}}}$

①$\alpha -{Fe}$为体心立方晶胞，晶胞边长为$a\;\rm pm$，体对角线长度为$\sqrt{3}{a\;\rm pm}$，体心立方晶胞中$\rm Fe$原子半径$ r$与体对角线关系为$ 4r=\sqrt{3}{a}$，因此$\rm {Fe}$原子的半径为$\dfrac{\sqrt{3}{a}}{4}\;\rm {pm}$。

②$\rm m$截面面积$S_{\rm m}=a^{2}\;\rm pm^{2}$，每个顶点被 ​​$\rm 8$个相邻晶胞共享​​，每个晶胞的顶点原子贡献$\dfrac{1}{8}$个原子给该晶面，所含原子数为$4\times \dfrac{1}{8}=0.5$，单位面积原子数为$\dfrac{1}{{2}{{{a}}^{2}}}$个$\rm pm^{-2}$；$\rm n$截面面积为${a}\times \sqrt{2}{a}=\sqrt{2}{{{a}}^{2}}\;\rm pm^{2}$，每个顶点被$\rm 8$个相邻晶胞共享，体心原子完全属于本截面，所含原子数为$\left( 4\times \dfrac{1}{8} \right)+1=1.5$，单位面积原子数为$\dfrac{3}{2\sqrt{2}{{{a}}^{2}}}=\dfrac{3\sqrt{2}}{{4}{{{a}}^{2}}}$个∙$\rm pm^{-2}$，因此催化活性较低的是$\rm n$截面，该截面单位面积含有的$\rm {Fe}$原子为$\dfrac{3\sqrt{2}}{{4}{{{a}}^{2}}}$个∙$\rm pm^{-2}$。