在圆锥$SO$中，$C$是母线$SA$上靠近点$S$的三等分点，$SA=l$，底面圆的半径为$r$，圆锥$SO$的侧面积为$3\pi$，则$(\qquad)$．

当$r=1$时，从点$A$绕圆锥侧面一周到点$C$的最小长度为$\\sqrt{13}$

当$r=\\dfrac{3}{2}$时，过顶点$S$和两母线的截面三角形的最大面积为$\\dfrac{3\\sqrt{7}}{4}$

当$l=3$时，圆锥$SO$的外接球表面积为$\\dfrac{8l\\pi }{8}$

当$l=3$时，棱长为$\\dfrac{2\\sqrt{3}}{3}$的正四面体在圆锥$SO$内可以任意转动

题意，$\pi lr=3\pi$，即$lr=3$，

对于$\rm A$，当$r=1$时，$l=3$，$CS=1$，圆锥的侧面展开图为如图所示的扇形，

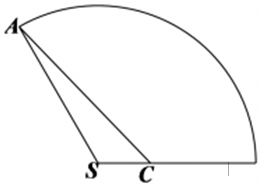
侧面展开图扇形弧长即为圆锥的底面圆周长$2\pi$，由扇形弧长公式可得则$\angle ASC=\dfrac{2\pi }{3}$，

在$\triangle ASC$中，由余弦定理得：$AC^{2}=AS^{2}+CS^{2}-2AS\cdot CS\cos \angle ASC=13$，即$AC=\sqrt{13}$，故$\rm A$正确；

对于$\rm B$，当$r=\dfrac{3}{2}$时，有$l=2$，令圆锥$SO$的轴截面等腰三角形顶角为$\theta$，$\cos \theta =\dfrac{{2}^{2}+{2}^{2}-{3}^{2}}{2\times 2\times 2}\lt 0$，

$\theta$为钝角，令$P$，$Q$是圆锥$SO$的底面圆周上任意的不同两点，则$0\lt \angle PSQ\leqslant \theta$，

$\therefore \triangle PSQ$的面积为$\dfrac{1}{2}{l}^{2}\sin \angle PSQ\leqslant \dfrac{1}{2}{l}^{2}\times \sin 90^\circ =2$，当且仅当$\angle PSQ=90^\circ$时取“$=$”，故$\rm B$不正确；

对于$\rm D$，棱长为$\dfrac{2\sqrt{3}}{3}$的正四面体$BDMN$可以补形成正方体$GBHD-MENF$，如图，

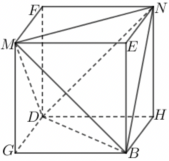
则正方体棱长$GB=\dfrac{\sqrt{2}}{2}BD=\dfrac{\sqrt{6}}{3}$，其外接球即正四面体$BDMN$的外接球直径为$\sqrt{2}$，球半径${R}_{1}=\dfrac{\sqrt{2}}{2}$，

当$l=3$时，$r=1$，圆锥$SO$的内切球球心在线段$SO$上，圆锥的轴截面截内切球得大圆，是圆锥轴截面等腰三角形内切圆，

设其半径为$r_{1}$，由三角形面积得：$\dfrac{1}{2}{r}_{1}(3+3+2)=\dfrac{1}{2}\times 2\times 2\sqrt{2}$，解得$r_{1}=\dfrac{\sqrt{2}}{2}$，$R_{1}=r_{1}$，

因此，半径为$\dfrac{\sqrt{2}}{2}$的球在圆锥$SO$内可以任意转动，

而棱长为$\dfrac{2\sqrt{3}}{3}$的正四面体的外接球的半径为$\dfrac{2\sqrt{3}}{3}\times \dfrac{\sqrt{6}}{4}=\dfrac{\sqrt{2}}{2}$，

故棱长为$\dfrac{2\sqrt{3}}{3}$的正四面体在半径为$\dfrac{\sqrt{2}}{2}$的球内可以任意转动，

$\therefore $ 当$l=3$时，棱长为$\dfrac{2\sqrt{3}}{3}$的正四面体在圆锥$SO$内可以任意转动，$\rm D$正确．

对于$\rm C$，当$l=3$时，$r=1$，圆锥$SO$的外接球球心在直线$SO$上，圆锥的底面圆是球的截面小圆，而圆锥的高$SO=\sqrt{{l}^{2}-{r}^{2}}=2\sqrt{2}$，

设外接球半径为$R$，则有$(R-SO)^{2}+r^{2}=R^{2}$，即$(R-2\sqrt{2})^{2}+1={R}^{2}$，解得$R=\dfrac{9\sqrt{2}}{8}$，其表面积为$4\pi {R}^{2}=\dfrac{81\pi }{8}$，$\rm C$正确．

故选：$\rm ACD$