某调查机构为了解市民对该市$5G$网络服务质量的满意程度，从使用了$5G$手机的市民中随机选取了$200$人进行了问卷调查，并将这$200$人根据其满意度得分分成以下$6$组：$\left[ 40,50 \right)$，$\left[ 50,60 \right)$，$\left[ 60,70 \right)$，…，$\left[ 90,100 \right]$，统计结果如图所示：

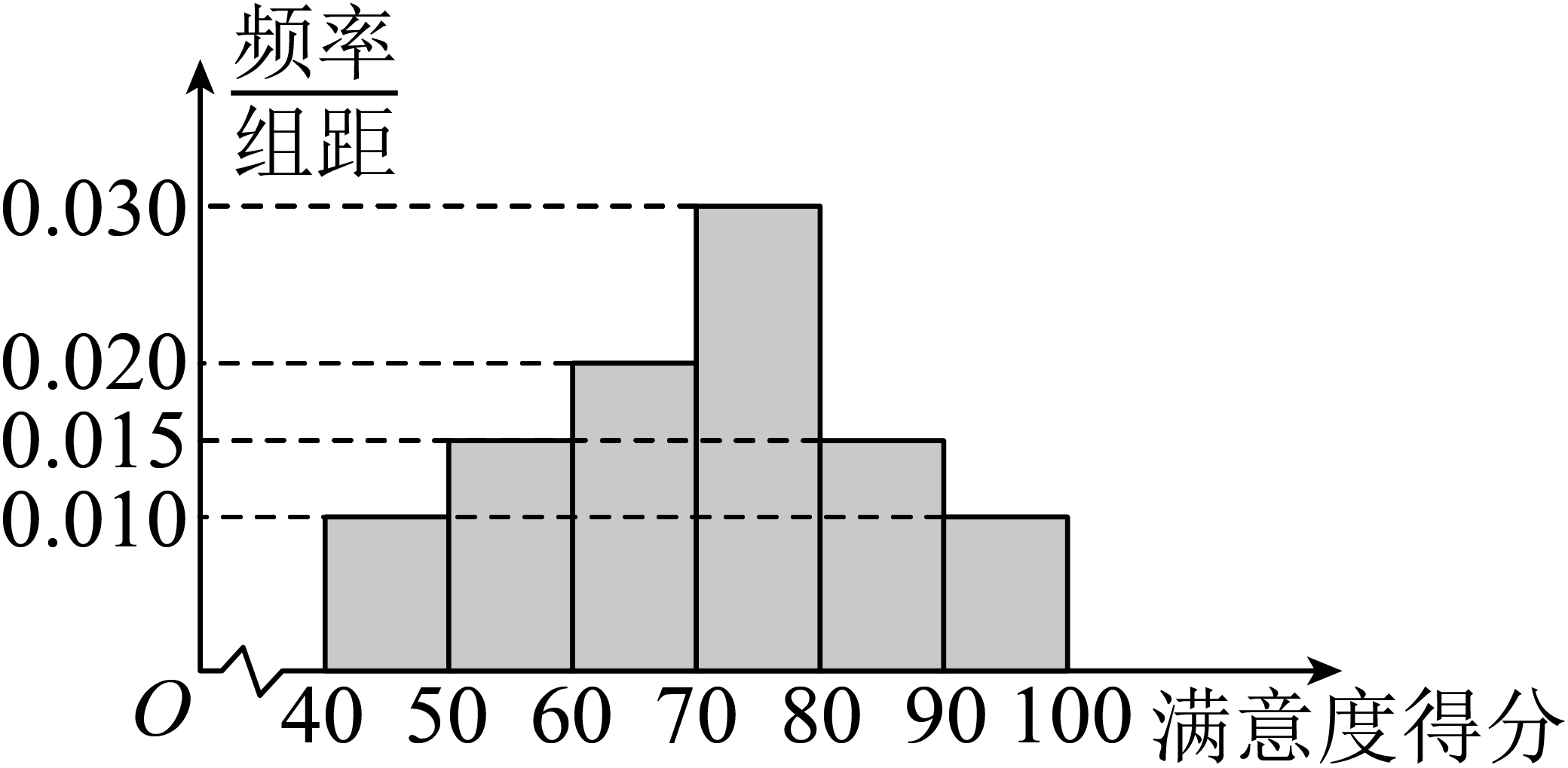
$(1)$由直方图可认为$A$市市民对$5G$网络满意度得分$z$（单位：分）近似地服从正态分布$N\left( \mu ,{{\sigma }^{2}} \right)$，其中$\mu $近似为样本平均数$\overline{x}$，$\sigma $近似为样本的标准差$s$，并已求得$s=14.31$．若$A$市恰有$2$万名$5G$手机用户，试估计这些$5G$手机用户中满意度得分位于区间$\left[ 56.19,99.12 \right]$的人数（每组数据以区间的中点值为代表）；

$(2)$该调查机构为参与本次调查的$5G$手机用户举行了抽奖活动，每人最多有$10$轮抽奖活动，每一轮抽奖相互独立，中奖率均为$\dfrac{1}{2}$．每一轮抽奖，若中奖，奖金为$100$元话费且继续参加下一轮抽奖；若未中奖，则抽奖活动结束，现小王参与了此次抽奖活动．

①求小王获得$900$元话费的概率；

②求小王所获话费总额$X$的数学期望（结果精确到$0.01$）．

参考数据：若随机变量$z$服从正态分布$N\left( \mu ,{{\sigma }^{2}} \right)$，即$z\sim N\left( \mu ,{{\sigma }^{2}} \right)$，则$P\left( \mu -\sigma \le z\le \mu +\sigma \right)\approx 0.6827$，$P\left( \mu -2\sigma \le z\le \mu +2\sigma \right)\approx 0.9545$．

$(1)$$16372$（人）

$(2)$①$\\dfrac{1}{1024}$ ；②$99.90$（元）

$(1)$依题意，样本平均数为$\overline{x}=45\times 0.1+55\times 0.15+65\times 0.2+75\times 0.3+85\times 0.15+95\times 0.1=70.5$，即$\mu =\overline{x}=70.5$，

由$\sigma =s=14.31$，得$\left[ \mu -\sigma ,\mu +2\sigma \right]=\left[ 56.19,99.12 \right]$，

而$P(\mu -\sigma \le z\le \mu +2\sigma )=\dfrac{1}{2}P(\mu -\sigma \le z\le \mu +\sigma )+\dfrac{1}{2}(\mu -2\sigma \le z\le \mu +2\sigma )\approx 0.8186$，

$\therefore $ $2$万名$5G$手机用户中满意度得分位于区间$\left[ 56.19,99.12 \right]$的人数约为$20000\times 0.8186=16372$（人）．

$(2)$①小王获得$900$元话费表明其前$9$轮连续中奖且第$10$轮未中奖，

$\therefore $ 所求的概率为$P={{\left(\dfrac{1}{2}\right)}^{9}}\times \dfrac{1}{2}=\dfrac{1}{1024}$．

②依题意，$X$的可能取值有$0$，$100$，$200$，$300$，$400$，$500$，$600$，$700$，$800$，$900$，$1000$，即$X=100i$，$0\le i\le 10$，$i\in \bf{N}$，

当$1\le i\le 9$，$i\in \bf{N}$时，$X=100i$，说明小王前$i$轮连续中奖且第$i+1$轮未中奖，此时$P(X=100i)={{\left(\dfrac{1}{2}\right)}^{i}}\cdot \dfrac{1}{2}=\dfrac{1}{{{2}^{i+1}}}$，

又$P\left( X=0 \right)=\dfrac{1}{2}$满足$P(X=100i)={{\left(\dfrac{1}{2}\right)}^{i}}\cdot \dfrac{1}{2}=\dfrac{1}{{{2}^{i+1}}}$，$P(X=1000)=\dfrac{1}{{{2}^{10}}}$，

因此$P\left( X=100i \right)=\begin{cases} \dfrac{1}{{{2}^{i+1}}},0\le i\le 9,i\in \bf{N} \\ \dfrac{1}{{{2}^{10}}},i=10 \\ \end{cases}$，于是$E(X)=0\times \dfrac{1}{2}+\left(\dfrac{1}{{{2}^{2}}}+\dfrac{2}{{{2}^{3}}}+\dfrac{3}{{{2}^{4}}}+\cdot \cdot \cdot +\dfrac{9}{{{2}^{10}}}\right)\times 100+\dfrac{1000}{{{2}^{10}}}$，

令$S=\dfrac{1}{{{2}^{2}}}+\dfrac{2}{{{2}^{3}}}+\dfrac{3}{{{2}^{4}}}+\cdots +\dfrac{9}{{{2}^{10}}}$，则$\dfrac{1}{2}S=\dfrac{1}{{{2}^{3}}}+\dfrac{2}{{{2}^{4}}}+\dfrac{3}{{{2}^{5}}}+\cdots +\dfrac{9}{{{2}^{11}}}$，

两式相减得$\dfrac{1}{2}S=\dfrac{1}{{{2}^{2}}}+\dfrac{1}{{{2}^{3}}}+\dfrac{1}{{{2}^{4}}}+\cdots +\dfrac{1}{{{2}^{10}}}-\dfrac{9}{{{2}^{11}}}=\dfrac{\dfrac{1}{{{2}^{2}}}\left(1-\dfrac{1}{{{2}^{9}}}\right)}{1-\dfrac{1}{2}}-\dfrac{9}{{{2}^{11}}}=\dfrac{1}{2}-\dfrac{1}{{{2}^{10}}}-\dfrac{9}{{{2}^{11}}}=\dfrac{1}{2}-\dfrac{11}{{{2}^{11}}}$，

化简得$S=1-\dfrac{11}{{{2}^{10}}}$，则$E(X)=\left(1-\dfrac{11}{{{2}^{10}}}\right)\times 100+\dfrac{1000}{{{2}^{10}}}=100-\dfrac{25}{{{2}^{8}}}\approx 99.90$（元），

$\therefore $ 小王所获话费总额$X$的数学期望为$99.90$元．