一长为$L$的直导线置于磁感应强度大小为$B$的匀强磁场中，导线中的电流为$I$。下列说法正确的是 $(\quad\ \ \ \ )$

通电直导线受到的安培力大小为$BIL$

无论通电直导线如何放置，它都将受到安培力

通电直导线所受安培力的方向垂直于磁感应强度方向和电流方向构成的平面

安培力是载流子受到的洛伦兹力的宏观表现，所以安培力对通电直导线不做功

$\rm AB$$.$根据安培力计算公式：$F=BIL\sin\theta$（$\theta$为直导线与磁场方向的夹角），当$\theta≠90^\circ$时，通电直导线受到的安培力大小不等于$BIL$；当$\theta≠0^\circ$时，通电直导线不受安培力作用，故$\rm AB$错误；

$\rm C$$.$根据左手定则可知通电直导线所受安培力的方向垂直于磁感应强度方向和电流方向构成的平面，故$\rm C$正确；

$\rm D$$.$安培力是载流子受到的洛伦兹力的宏观表现，安培力对通电直导线是可以做功的，故$\rm D$错误。

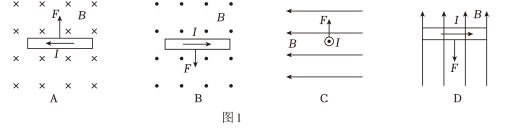
在下列如图$1$四幅图中，能正确标明通电直导线所受安培力$F$方向的是                 。

$B$

根据左手定则可知，选项$A$中的通电直导线所受安培力$F$方向向下；选项$B$中的通电直导线所受安培力$F$方向向下；选项$C$中的通电直导线所受安培力$F$方向向下；选项$D$中的通电直导线所受安培力$F$方向垂直纸面向外，故$\rm B$正确，$\rm ACD$错误。

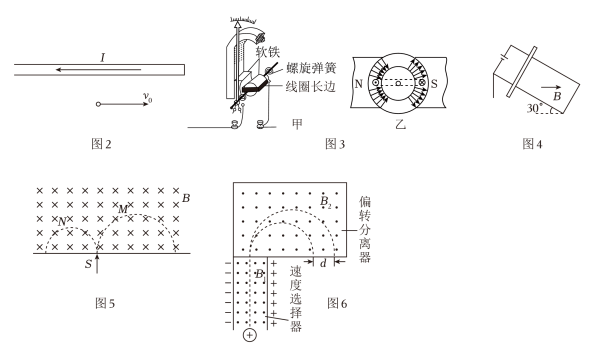
一根通电直导线水平放置，通过直导线的恒定电流方向如图$2$所示，现有一电子从直导线下方以水平向右的初速度$v_{0}$开始运动，不考虑电子重力，关于接下来电子的运动，下列说法正确的是 $(\quad\ \ \ \ )$

电子将向下偏转，运动的半径逐渐变大

电子将向上偏转，运动的半径逐渐变小

电子将向上偏转，运动的半径逐渐变大

电子将向下偏转，运动的半径逐渐变小

根据安培定则可知通过直导线的恒定电流产生的磁场在导线下方的方向垂直纸面向外，电子带负电，根据左手定则，可知电子受到向上的洛伦兹力作用，则电子将向上偏转，越靠近直导线磁感应强度越大，根据洛伦兹力提供向心力可得$eBv=m\dfrac{v^{2}}{r}$，解得电子运动半径$r=\dfrac{mv}{eB}$，可知运动半径逐渐变小，故$\rm B$正确，$\rm ACD$错误。

某磁电式电流表结构如图$3$甲所示，矩形线圈匝数为$n$，长边长度为$l$。矩形线圈放在均匀辐射状磁场中，如图$3$乙所示，两条长边经过的位置磁感应强度大小为$B$。当线圈长边中电流为$I$时，电流表指针偏转的角度为$\theta$，则当电流表指针偏转的角度为$2\theta$时，线圈一侧长边受到的安培力大小为 $(\quad\ \ \ \ )$

2nBIl

nBIl

2BIl

BIl

磁电式电流表指针偏转的角度与通过的电流成正比，则当指针偏转的角度为$2\theta$时，线圈中的电流为$2I$，则一侧长边受到的安培力大小为$F=nB\cdot 2Il=2nBIl$，故$\rm A$正确，$\rm BCD$错误。

如图$4$所示，两光滑金属导轨倾斜放置，与水平面夹角为$30^\circ$，导轨间距为$L$，一质量为$m$的导体棒与导轨垂直放置，电源输出电流保持恒定，不计导轨电阻。当磁场水平向右时，导体棒恰能静止，现磁场发生变化，方向沿逆时针旋转，最终竖直向上，在磁场变化的过程中，导体棒始终静止，关于$B$的大小的变化说法正确的是 $(\quad\ \ \ \ )$

逐渐增大

逐渐减小

先增大后减小

先减小后增大

磁场由水平方向沿逆时针旋转到竖直向上的过程，对应的安培力的方向由竖直向上逆时针旋转到水平向左，如下图所示，

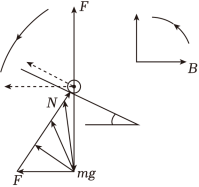
导体棒始终静止，重力、安培力$F$、支持力$N$三力平衡，作出这三个力组成的矢量三角形，如上图所示，可得此过程安培力$F$先减小后增大，当$F$与$N$方向垂直时安培力最小，由安培力计算公式可知$B$的大小先减小后增大，故$\rm D$正确，$\rm ABC$错误。

如图$5$所示，质量和电荷量大小都相等的带电粒子$M$和$N$，以不同的速率经小孔$S$垂直射入有界匀强磁场，磁场方向垂直纸面向里，$M$和$N$运行的半圆轨迹如图中的虚线所示，则$M$带                 （选填“正电”或“负电”）；$M$的运行时间                 $\;\rm N$的运行时间（选填“$\gt $”、“$=$”或“$\lt $”）。

带电粒子$M$顺时针偏转，射入磁场时所受洛伦兹力向右，由左手定则可知$M$带负电。

带电粒子$M$和$N$的质量$m$和电荷量$q$都相等，粒子在磁场中做匀速圆周运动的运动周期$T=\dfrac{2\pi m}{qB}$，可见两个粒子的运动周期相同，$M$和$N$运行轨迹均为半圆，运动时间均为周期的一半，$M$的运行时间等于$N$的运行时间。

图$6$为质谱仪的示意图。速度选择器的匀强电场强度$E$为$1.2\times 10^{5}\;\rm N/C$，匀强磁场的磁感应强度$B_{1}$为$0.6T$（电场方向与磁场方向相互垂直）。偏转分离器的磁感应强度$B_{2}$为$0.8T$。（已知质子质量为$1.67\times 10^{−27}\;\rm kg$，元电荷的电荷量为$e=1.60\times 10^{−19}\;\rm C$）试求：

（$i$）能通过速度选择器的粒子速度的大小；

（$ii$）如质子和氘核以相同速度进入偏转分离器，试求在质谱仪底片上收集到的条纹之间的距离$d$；

（$iii$）求质子和氘核在磁场中运动的时间。

（$i$）能通过速度选择器的粒子速度的大小为$2\\times 10^{5}\\;\\rm m/s$；

（$ii$）在质谱仪底片上收集到的条纹之间的距离$d$为$5.22\\times 10^{﹣3}\\;\\rm m$；

（$iii$）质子和氘核在磁场中运动的时间分别为$1.31\\pi\\times 10^{﹣8}\\;\\rm s$、$2.61\\pi\\times 10^{﹣8}\\;\\rm s$

（$i$）能通过速度选择器的粒子在其中做直线运动，所受电场力与洛伦兹力等大反向，则有：

$qE=qB_{1}v$，解得：$v=\dfrac{E}{{{B}_{1}}}=\dfrac{1.2\times {{10}^{5}}}{0.6}m/s=2\times 10^{5}m/s$；

（$ii$）质子和氘核在偏转分离器中均做匀速圆周运动，根据洛伦兹力提供向心力可得：$qB_{2}v=m\dfrac{{{v}^{2}}}{r}$

解得运动半径：$r=\dfrac{mv}{q{{B}_{2}}}$

质子的质量为$1.67\times10^{−27}\;\rm kg$，电荷量为$1.60\times 10^{−19}\;\rm C$

解得质子的运动半径为：$r_{1}≈2.61\times 10^{-3}\;\rm m$

氘核的质量为$2\times 1.67\times 10^{-27}\;\rm kg$，电荷量为$1.60\times 10^{−19}\;\rm C$

解得氘核的运动半径为：$r_{2}≈5.22\times 10^{-3}\;\rm m$

根据几何关系可得在质谱仪底片上收集到的条纹之间的距离$d=2r_{2}﹣2r_{1}$

解得：$d=5.22\times 10^{-3}\;\rm m$

（$iii$）粒子在磁场中做匀速圆周运动的运动周期$T=\dfrac{2\pi m}{q{{B}_{2}}}$

代入数据可得质子的运动周期$T_{1}≈2.61\pi\times 10^{-8}\;\rm s$

氘核的运动周期$T_{2}≈5.22\pi\times 10^{-8}\;\rm s$

质子和氘核运动轨迹均为半圆，运动时间均为各自周期的一半，则

质子在磁场中运动的时间$t_{1}=\dfrac{1}{2}T_{1}=\dfrac{1}{2}\times 2.61\pi\times 10^{-8}\;\rm s≈1.31\pi\times 10^{-8}\;\rm s$

氘核在磁场中运动的时间$t_{2}=\frac{1}{2}T_{2}=\frac{1}{2}\times5.22\pi\times10^{-8}s\approx2.61\pi\times10^{-8}s$