如图所示，在绝缘水平面上放置一可视为质点的带正电滑块，滑块的质量为$m$、电量为$q$，橡皮筋的一端固定在$O$点，另一端拴住滑块，$O$点的正下方$A$处有一垂直于纸面且位于橡皮筋右侧的固定光滑细杆，$OA$为橡皮筋的自然长度。橡皮筋的弹力与伸长量成正比，劲度系数为$k$。现在滑块所在的区域加水平向右的匀强电场$E$，滑块从$A$点正下方的$B$点由静止开始运动，刚好能运动到$C$点。已知整个过程中滑块对水平面始终有压力，滑块在$B$点时橡皮筋的伸长量为$h$，$B$点到$C$点的距离为$L$，重力加速度为$g$，下列说法正确的是$(\qquad)$

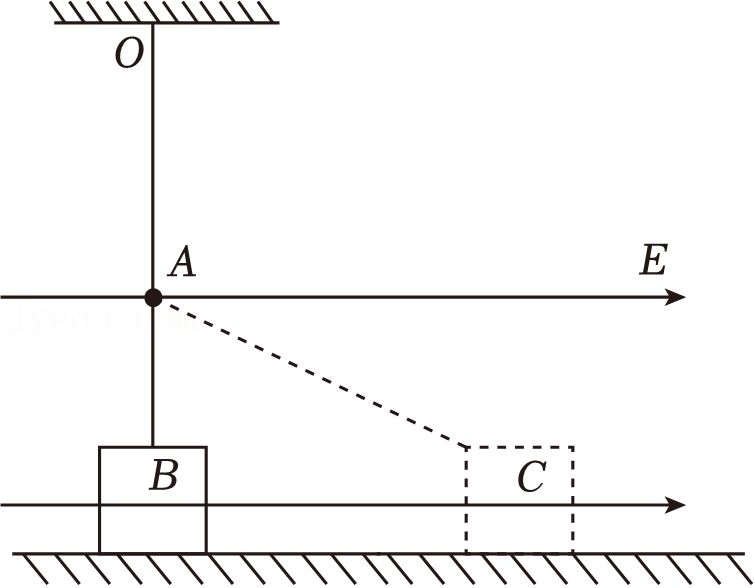
滑块从$B$到$C$的运动过程中所受水平面的摩擦力变小

滑块从$B$运动到$C$的过程中，加速度先减小后增大

滑块从$B$运动到$C$的过程中，滑块克服橡皮筋弹力做功$kL^{2}$

滑块与水平面间的动摩擦因数为$\\dfrac{2Eq - kL}{2(mg - kh)}$

$\rm A$、滑块在$BC$过程中的某一点$D$处，若橡皮筋的伸长量为$x$，则橡皮筋的弹力：$F=kx$，受力分析如下：

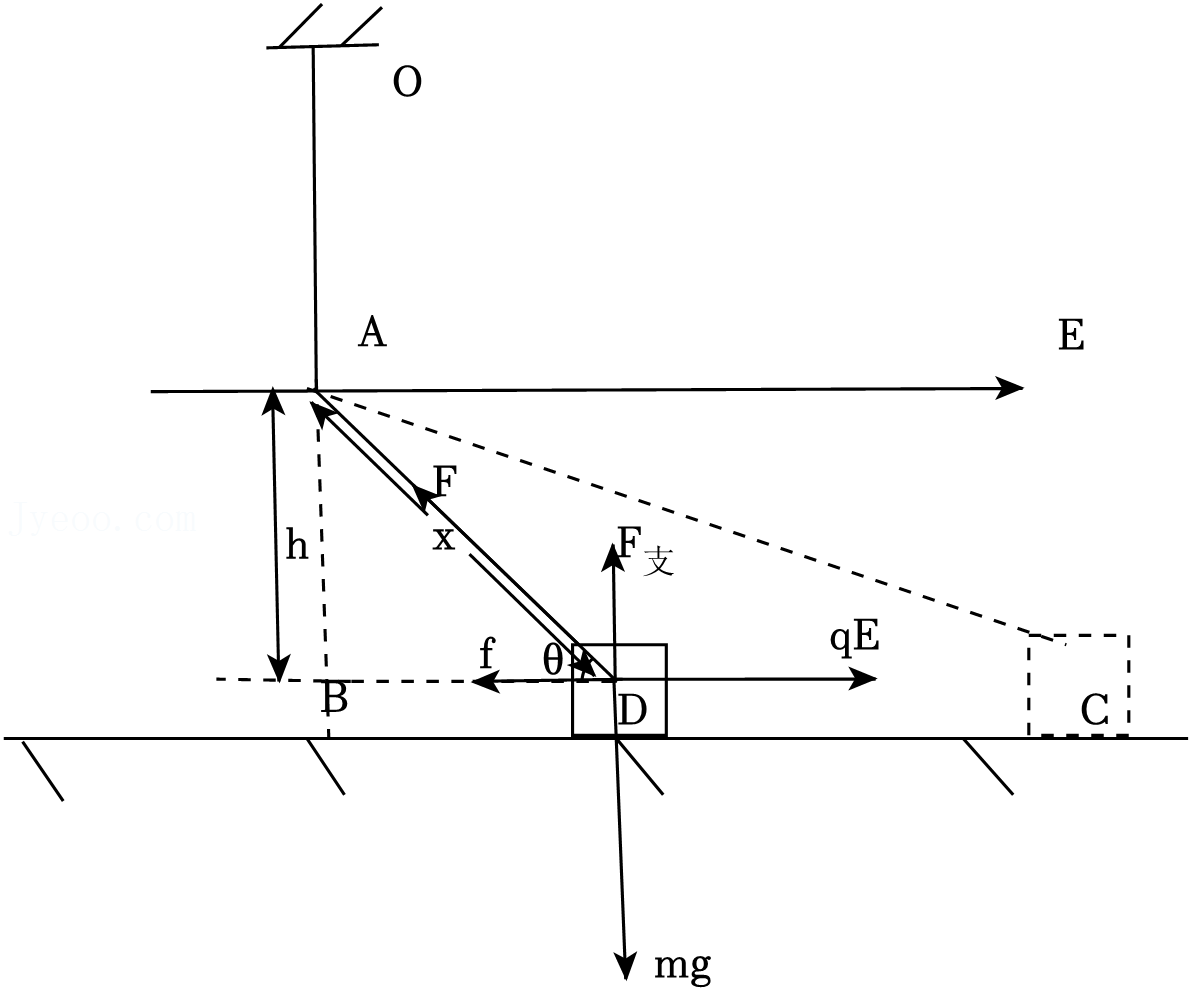
在竖直方向上：$F_{支}+kx\cdot \sin\theta=mg$，水平方向上：$qE-kx\cdot \cos\theta-f=ma$，

由相互作用力可知：$F_{支}=F_{压}$，$f=\mu F_{压}$，

解得：$f=\mu (mg-kh)$，故摩擦力$f$不变，故$\rm A$错误；

$\rm B$、由$\rm A$选项分析可知：$a = \dfrac{qE - f - kx \cdot \cos\theta}{m}$，滑块从$B$到$C$的过程中，$qE$不变，$f$不变，$k$不变，$m$不变，$x\cdot \cos\theta$在变大；

初始滑块能向右移动，即合力向右，随$x\cdot \cos\theta$变大，$a$减小；

后来滑块刚好到$C$，即经历了减速过程，到$C$时刚好减速为$0$，即在减速过程中，$a$的大小为：$a = \dfrac{kx \cdot \cos\theta + f - qE}{m}$，随$x\cdot \cos\theta$变大，$a$变大，故$\rm B$正确；

$\rm C$、滑块从$B$到$C$的过程中，由功能关系可知：$W_{弹} = \dfrac{1}{2}k(h^{2} + L^{2}) - \dfrac{1}{2}kh^{2}$，解得：$W_{弹} = \dfrac{1}{2}kL^{2}$，故$\rm C$错误；

$\rm D$、滑块从$B$到$C$的过程中，由动能定理：$qEL-\mu (mg-kh)L-W_{弹}=0-0$，解得：$\mu = \dfrac{2qE - kL}{2(mg - kh)}$，故$\rm D$正确。

故选：$\rm BD$。