某同学在“探究弹簧产生的弹力和形变量的关系”的实验中。用图$a$所示实验装置，改变悬挂在弹簧下端钩码的质量$m$，分别测出平衡时对应弹簧的长度$L$，得到一系列数据，并绘制出$L-m$图像，如图$b$所示。通过对数据分析知道：

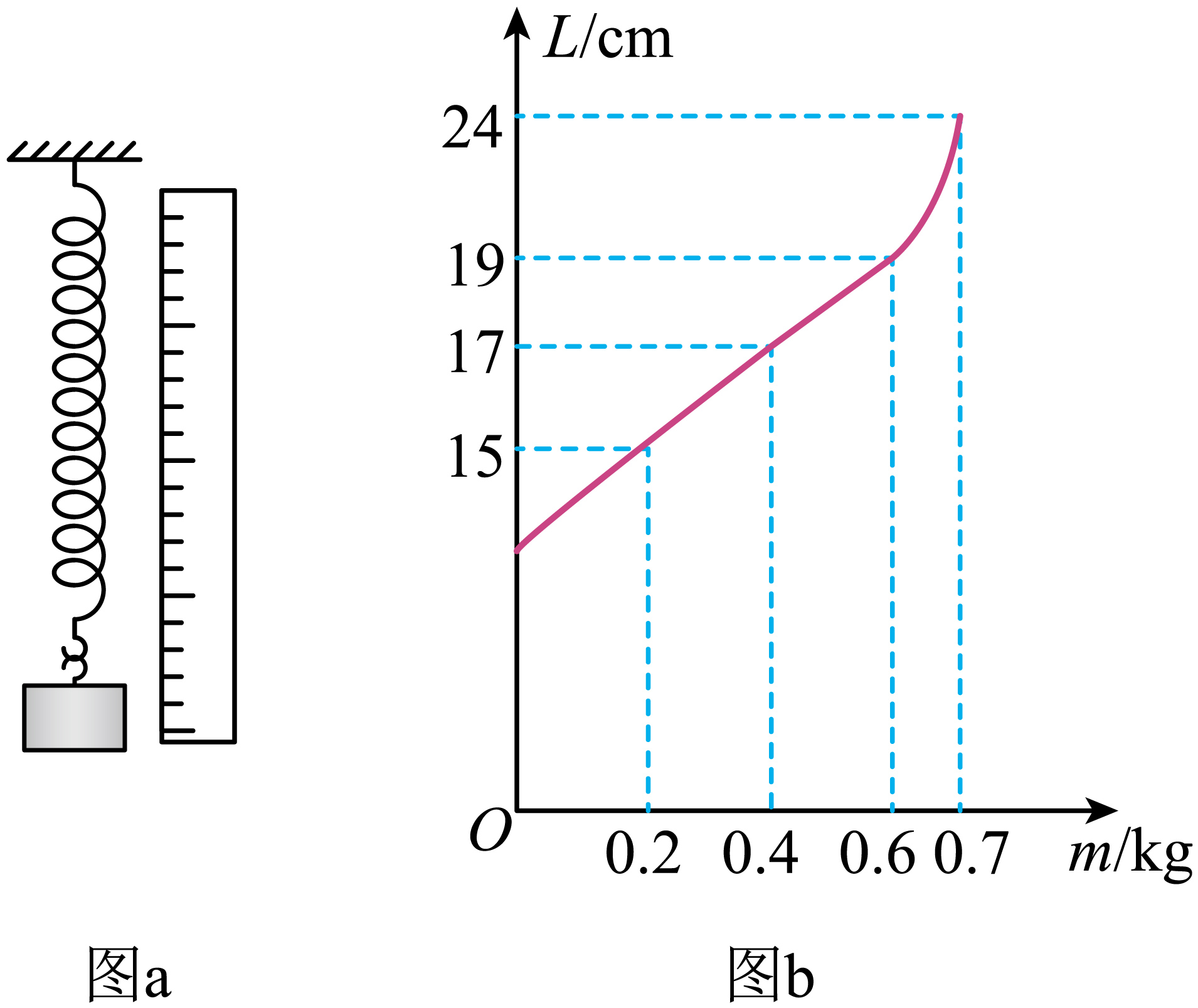
①在正常情况下该弹簧的劲度系数$k=$                 ${\text{N}}/{\text{m}}$。

②简答题：

$\rm i$．从图像分析中发现，最后一组数据点明显偏离胡克定律，出现这一现象的原因可能是                 。

$\rm ii$．为什么可以用钩码的重力来表示弹簧形变时产生的弹力？                 

①在正常情况下该弹簧的劲度系数$k=\dfrac{F}{\Delta L}=\dfrac{mg}{\Delta L}= \dfrac{(0.6-0.2) \times 10}{(19-15) \times 10^{- 2}}\;\rm N/m=100\;\rm N/m$

②$\rm i$．从图像分析中发现，最后一组数据点明显偏离胡克定律，出现这一现象的原因可能是拉力超出了弹簧的弹性限度。

$\rm ii$．砝码平衡时，砝码的重力和弹簧的拉力是一对平衡力，大小相等，所以可以用钩码的重力来表示弹簧形变时产生的弹力。

质量为$m$的蹦极爱好者身系一根弹性绳，从高空某点静止开始自由下落，下降高度$h$后弹性绳开始对人产生弹力，再经历时间$t$，人到达最低点。整个运动过程始终沿竖直方向。则在时间$t$内，弹性绳的$(\qquad)$

弹性势能增加量为$mgh$

平均作用力等于$\\dfrac{m\\sqrt{2gh}}{t}+mg$

最大伸长量一定为$h$

弹力的最大值大于$2mg$

$\rm AC$．由能量关系可知，弹性势能增加量为$\Delta E_{P}=mg(h+h')$

其中$h'$是从弹性绳开始伸直到最低点时下落的高度，因弹性绳的劲度系数未知，弹性绳的最大伸长量不一定为$h$，选项$\rm AC$错误；

$\rm B$．弹性绳刚伸直时的速度$v=\sqrt{2gh}$

设向上为正，从弹性绳开始伸直到最低点由动量定理$Ft-mgt=0-(−mv)$

解得平均作用力$F=\dfrac{m\sqrt{2gh}}{t}+mg$

选项$\rm B$正确；

$\rm D$．假设在弹性绳刚伸直时人的速度为零，则到达平衡位置时弹性绳的弹力为$mg$，则到最低点时弹力的最大值等于$2mg$，因在弹性绳刚伸直时人的速度大于零，可知到最低点时弹力的最大值大于$2mg$，选项$\rm D$正确。

故选：$\rm BD$。

已知弹簧的弹性势能大小为$E_{\text{p}} =\dfrac{1}{2}kx^{2}$，如图所示，一劲度系数为$k=2 \times 10^{2}\;\rm N/m$的轻弹簧一端固定，另一端连接一个质量$m=0.5\;\rm kg$的物块，静止在弹簧原长位置$O$点。物块与桌面间的动摩擦因数为$\mu =0.6$。现用一个$F=10\;\rm N$的恒定拉力，使物块开始向右运动。求物块完全停下来之前：

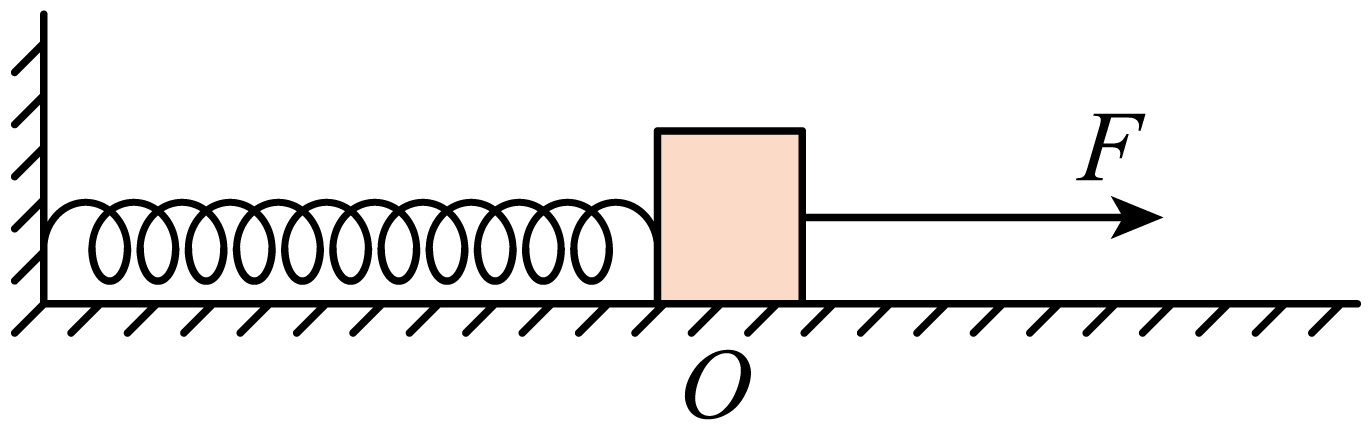
①物块处于平衡时弹簧的伸长量$x$；

②物块的最大速度$v_{\rm m}$；

③弹簧的最大伸长量$x_{\rm m}$。

①$3.5\\;\\rm cm$或$6.5\\;\\rm cm$；②$v_{\\rm m}=0.7\\;\\rm m/s$；③$x_{\\rm m}=7\\;\\rm m$

①在向右运动过程中，摩擦力向左，$F=\mu mg+kx_{1} $，$x_{1}=3.5\;\rm cm $

在物块到达最右端后向左运动过程中，摩擦力向右，$F+\mu mg=kx_{2} $，$x_{2}=6.5\;\rm cm$

②当第一次达到平衡时速度最大，根据动能定理：$Fx_{1}-\mu mgx_{1}-\dfrac{k{x_{1}}^{2}}{2}=\dfrac{1}{2}m{v_{\text{m}}}^{2}$

解得$v_{\rm m}=0.7\;\rm m/s$

③当物块到达最右端时，速度为$0$，根据振动的对称性，最大伸长量为$x_{m}=2x_{1}=7\;\rm cm$

或：$Fx_{\text{m}}-\mu mgx_{\text{m}}=\dfrac{kx_{\text{m}}^{2}}{2}$

解得$x_{\rm m}=7\;\rm cm$