如图甲所示，小明先用$F_{1}=13\;\rm N$水平向右的力将一质量为$2\;\rm kg$的木箱向右移动$4\;\rm m$的距离后，在另一水平推力$F_{2}$作用下，又匀速运动$4\;\rm m$的距离到达斜面底端，撤去外力，之后冲上倾角为$37^\circ$的斜面，物体的动能随运动距离变化的图像如图乙。已知木箱与斜面间的摩擦因数为$0.5$，关于物体的运动，下列说法中正确的是$(\qquad)$

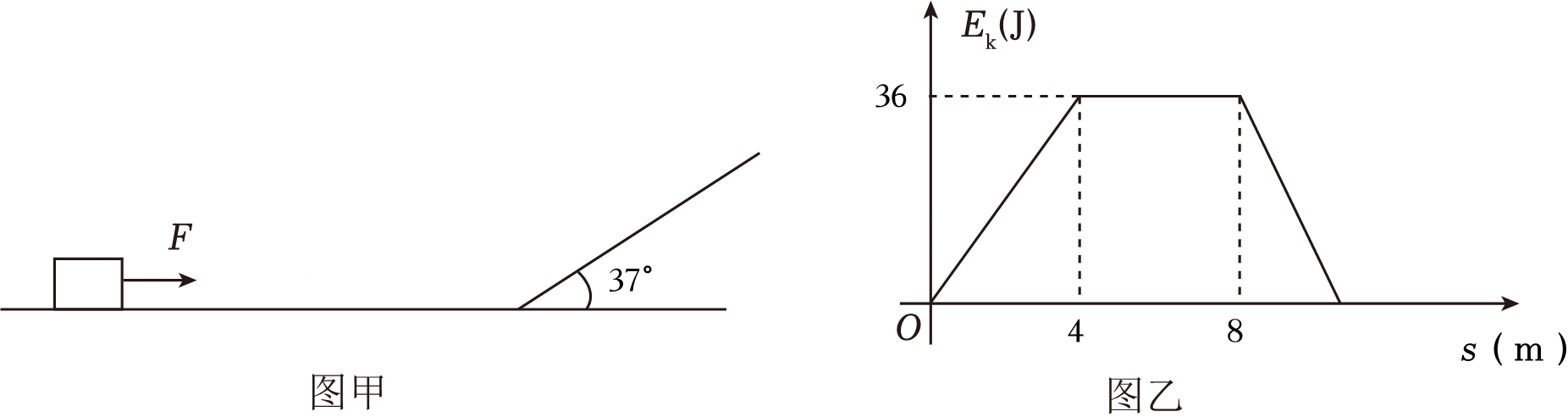
$F_{2}$的大小为$4\\;\\rm N$

木箱能到达斜面的最大高度为$1.8\\;\\rm m$

木箱返回水平面后向左运动的最大距离为$1.8\\;\\rm m$

整个运动过程中，克服摩擦力所做的功为$36\\;\\rm J$

$\rm A$、木箱在$x_{1}=4\;\rm m$内，摩擦力大小为$f_{1}$，根据动能定理可得：$(F_{1}-f_{1})x_{1}=E_{k}-0$，其中：$E_{k}=36\;\rm J$

在$4m\sim 8m$过程中，动能不变，则有：$F_{2}=f_{1}$，

代入数据解得：$F_{2}=f_{1}=4\;\rm N$，故$\rm A$正确；

$\rm B$、木箱冲上斜面后做匀减速运动，根据动能定理，有：$-(mg\sin\theta+\mu mg\cos\theta)x_{2}=0-E_{k}$

解得：$x_{2}=1.8\;\rm m$

所以木箱在斜面上能到达的最大高度为：$h=x_{2}\sin\theta=1.8\times 0.6\;\rm m=1.08\;\rm m$，故$\rm B$错误；

$\rm C$、木箱从冲上斜面到最终停下来，根据动能定理可得：$-\mu mg\cos\theta\cdot 2x_{2}-f_{1}x_{3}=0-E_{k}$

解得：$x_{3}=1.8\;\rm m$，故$\rm C$正确；

$\rm D$、对整个运动过程，由动能定理有：$F_{1}x_{1}+F_{2}x_{1}-W_{克}=0$

所以：$W_{克}=68\;\rm J$，故$\rm D$错误。

故选：$\rm AC$。