某人驾驶小型汽车行驶在平直的封闭测试道路上，$t=0$时刻开始无动力滑行，一段时间后以恒定功率加速行驶，车速达到最大后保持匀速，$v − t$图像如图所示。汽车与人的总质量为$1 \times 10^{3}\;\rm kg$，行驶中受到的阻力保持不变，则$(\qquad)$

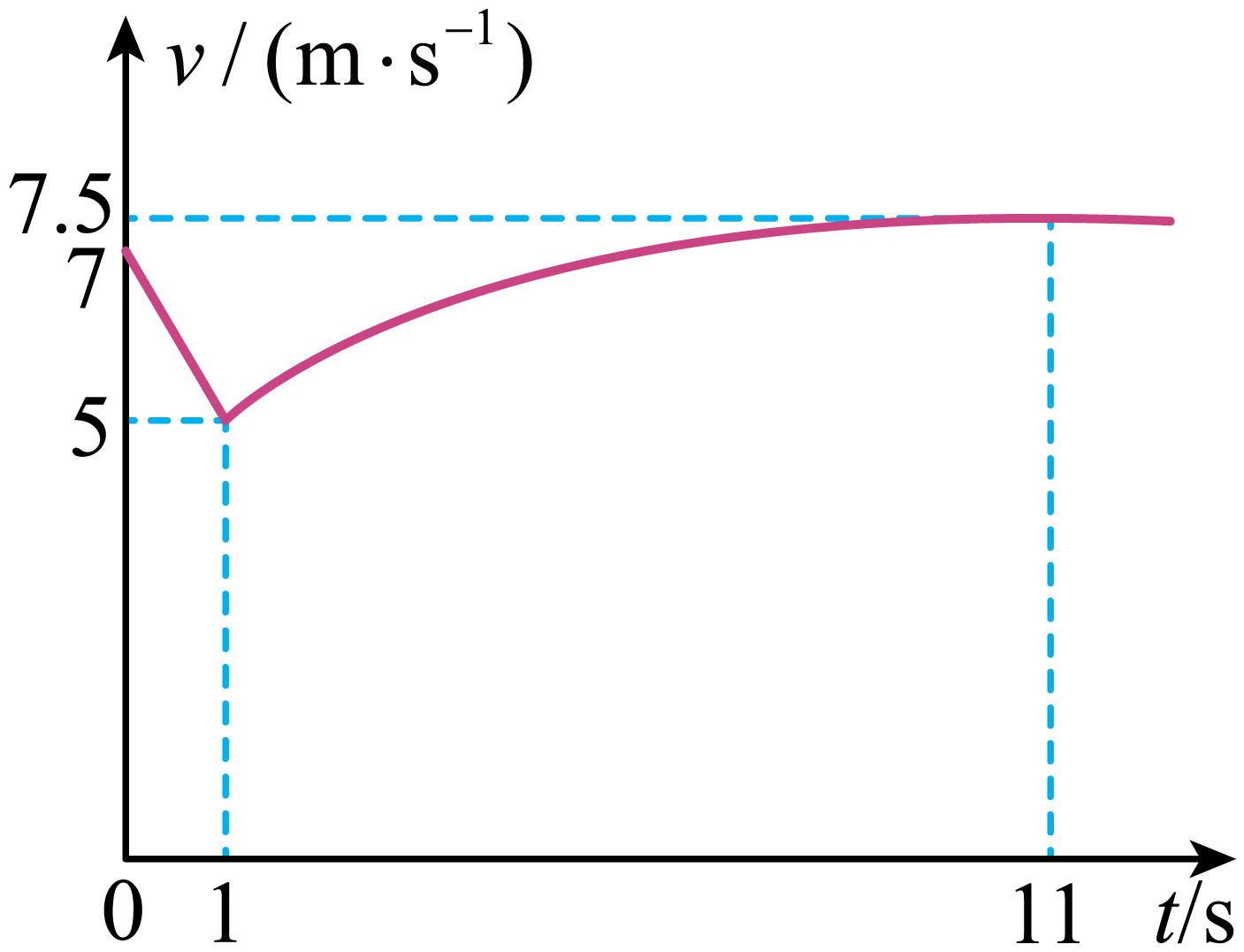
汽车行驶中所受阻力大小为$2 \\times 10^{3}\\;\\rm N$

$1\\;\\rm s ∼11\\;\\rm s$内汽车的功率为$10\\;\\rm kW$

$1\\;\\rm s ∼11\\;\\rm s$内汽车的位移为$75\\;\\rm m$

汽车加速过程中速度为$6\\;\\rm m/s$时的加速度大小为$0.5\\;\\rm m/s^{2}$

$\rm A$．根据题意，由图像可得，汽车无动力滑行时的加速度大小为$a_{1}=\dfrac{\Delta v}{\Delta t}=2\;\rm m/s^{2}$

由牛顿第二定律可得，汽车行驶中所受阻力大小为$f=ma_{1}=2 \times 10^{3}\;\rm N$，故$\rm A$正确；

$\rm B$．根据题意，由图可知，当$t=11\;\rm s$时，汽车达到最大速度$7.5\;\rm m/s$，此时汽车的牵引力为$F=f=2 \times 10^{3}\;\rm N$

汽车的功率为$P=Fv_{\rm m}=1.5 \times 10^{4}\;\rm W=15\;\rm kW$，故$\rm B$错误；

$\rm C$．根据题意，设$1\;\rm s ∼ 11\;\rm s$内汽车的位移为$x$，由动能定理有$P\left( t_{2}-t_{1} \right)-fx=\dfrac{1}{2}mv_{\text{m}}^{2}-\dfrac{1}{2}mv_{1}^{2}$

代入数据解得$x=67.1875\;\rm m$，故$\rm C$错误；

$\rm D$．汽车加速过程中速度为$6\;\rm m/s$时，牵引力为$F_{1}=\dfrac{P}{v}=2.5 \times 10^{3}\;\rm \text{N}$

由牛顿第二定律有$a=\dfrac{F_{1}-f}{m}=0.5\;\rm m/s^{2}$，故$\rm D$正确。

故选：$\rm AD$。